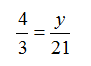Math 8 ( period 1)

Constant Rate of Change 3-1

Quick Review of Proportions

A proportion = 2 equal ratios ( 2 equivalent fractions)

Solve using equivalent fractions or cross multiplication and then a one-step equation

(see if you can simplify the fractions before you multiply)

Solve the proportion for y

Equivalent Fraction approach:

Multiply both the top and the bottom by 7

y = 28

Cross Products Approach

you will get

3y = (21)(4)

Now divide each side by 3

DO THIS BEFORE multiplying on the right side? WHY?  Because a lot of times you will be able to cross cancel and keep the numbers smaller. IT will be easier for you! y = 28

Quick review of Coordinate Plane:
Formed by 2 perpendicular number lines that intersect at 0.

Origin: The point (0,0) where the number lines intersect

x axis: The horizontal line

y axis: the vertical line

ordered pair: a pair of numbers that finds a location on the coordinate plane with x first and y listed second

x coordinate: the first number in the ordered pair that tells you how far to go the right ( or left)

y coordinate:  The second number in the ordered pair that tells you how far to go up ( or down) 

Graph: Locating points on the coordinate plane to help see the patterns (if any) between the points.

You can express the points first in a table of ordered pairs before you graph

Here’s an example about the cost of photo CD’s where the ordered pair (x, y) represents (number of CD’s, cost of CDs in dollars)

The sets of pairs

(1,$3), ( 2, $6) (3, $9)

Make a table

# of CDs	Cost in $	(x, y)
1	3	( 1, 3)
2	6	(2, 6)
3	9	(3, 9)

Graph the table and you will see that the points appear to be on a straight diagonal line that slopes up from the left and to the right.

Is there a pattern?     Yes

Each point is one unit to the right and 3 units up from the previous point. What does that mean in terms of the info about the CD’s?

It means that every time this company makes another CD it costs them $3  more 
This is called LINEAR RELATIONSHIP

Notice that the word linear contains the root word LINE

In order to have a graph that is a line, there must be a constant rate of change between the change in both pieces of the data.

In the above example, the two data items are cost and number of CD’s As the cost goes up 3, the number of CD’s goes up 1… every single time—constantly!!

So it has a constant rate of change. You make this into a ratio where you always place the change in the y value ( the up or down data) over the change in the x-value ( the right or left data)

So the constant rate of change for the above examples is 3/1 or $ 3/ CD

Wait—this is the unit cost!! YES IT IS!!!

Your book shows another example where Marcus downloads 2 songs each minute on his phone

The Unit Rate for this is 2 songs/ minute

If we turn this into a graph, we would graph  the following points ( minutes, number of songs)

(0 min, 0 songs) ( 1 min, 2 songs) (2 min, 4 songs) ( 3 min 6 songs)  etc

The CONSTANT RATE OF CHANGE on the graph:

As the number of songs goes UP 2 each time, the minutes go to the RIGHT 1

Making that into a ratio up 2/ over 1 = 2/1

That’s familiar because it’s the UNIT RATE: 2 songs/ 1 minute

How can you easily tell whether it is a constant rate of change and therefore linear?  If you graph it… it will be a diagonal line.

From the TABLE, you see the difference  (change in each row)… If this is constant, you have a linear relationship.

In the Marcus example, you would have + 2, + 2, + 2, +2 etc  on the songs row and + 1, + 1, + 1, +1 etc on the minutes row.

YOU CAN HAVE A NEGATIVE  Constant Rate of Change

Your book gives the example of taking money out of the bank at a constant rate… or it could be a pool emptying of water at a constant rate.

Now the y value is going DOWN constantly  ( or is NEGATIVE) the graph will still be a gdiagonal, but it will look like it is going DOWN from left to right.

You can use tables and graphs to compare different ratios

Let’s say that in the previous example there is another company that has higher costs and so it costs $4 not $3  for each CD You can produce another table:

# of CDs	Cost in $	(x, y)
1	4	( 1, 4)
2	8	(2, 8)
3	12	(3, 12)

Now  graph of these ordered pairs and compare it to the other company’s graph. Again it is a diagonal line going up to the right But this line is STEEPER.. for every unit to the right, it increases 4 units up… not 3 units… making it steeper WHY?  Because the cost  is higher..

PROPORTIONAL LINEAR RELATIONSHIPS

Linear relationships with a constant rate of change are PROPORTIONAL if they go through the ORIGIN (0,0) 

There are 2 ways to show this…on the graph see if it goes through the origin.. plug and chug to see if ( 0,0) works. or compare several points placing the y value over the x value as a ration… those ratios need o be in the same to be proportion

REMEMBER: The definition of a proportion is 2 equal ratios

The book gives an example which we talked about in class
Look again at page 173

Fahrenheit and Celsius temperatures

It is a LINEAR RELATIONSHIP (a diagonal line) with a CONSTANT RATE OF CHANGE  (9/5) But it is not PROPORTIONAL because it does NOT go through the origin  and if you simplify a few ratios, they are NOT equivalent