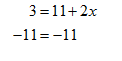Math 7 (Period 4)

Solving Equations With Variables on Both Sides 4.5

Some equations such as 2x + 3 = 3x + 5 have variables on both sides of the equal side. You will need to collect like variables on the SAME side!!

2x + 3 = 3x + 5

It is really your choice which other the variables you move Most students like to keep  the variable’s coefficient positive, so in this case you would subtract 2x from both sides

3 = 3x -2x+ 5

3 = x + 5

now you would subtract 5 from both sides… make sure to show each step

3-5 = x + 5 -5  ( would be how you would show it horizontally.)

-2 = x

So the solution is x = -2

Using the Distributive Property

Solve

8n – 4 = 3(2n + 8)

Use the Distributive Property

8n -4 = 6n + 24

Subtract 6n from both sides

8n -4 -6n = 6n + 24 -6n

2n – 4 = 24

Add4 to both sides

2n – 4 + 4 = 24 + 4

2n = 28

Divide both sides by 2

2n/2= 28/2

n = 14

Math 7 (Period 4)

Solving Equations Using the Distributive Property 4.4

You may need to use the Distributive Property in solving some equations.

Solve

 5y + 2(y-3) = 92

Use the distributive property to obtain

5y + 2y – 6 = 92

Combine like terms

7y – 6 = 92

Add six to both sides

7y = 98

 

y = 14

Solve 13 = 4(3x-7) +5

Again use the Distributive Property

13 = 12x – 28 + 5

Combine like terms

13 = 12x – 23

You will need to add 23 to both sides

36 = 12x

3= x

Solving with a Negative Coefficient

3 –(x-2) = 4

First realize this is really

3 -1(x-2) =4

In Algebra we call this The Inverse Property of a SUM. When you distribute the negative 1, everything inside the parentheses becomes it’s opposite.

So 3 -1(x-2) =4 becomes

3 –x + 2 = 4

Combine like terms

5 –x = 4

Using the methods from our previous lesson,

you could add x to bother sides, first

5 =4 + x

1 = x

Solving a multi-step problem often using the Distributive Property as well.

Math 7 (Period 4)

Solving Equations Involving Negative Coefficients 4.3

The following show two different methods for solving an equation involving a negative coefficient. You can use whichever method you prefer.

Solve 8 – x = 3

First please note--> that the 8 is positive. Many students attach the negative sign to the 8.
That is NOT CORRECT! The subtraction sign (or negative sign) is attached to the x.
It is really -1 times x but we simply write –x. The -1 is understood to be part of the coefficient.

You can rewrite it so that you read...

Method 1

8 + (-1)x = 3

Now you need to isolate the variable—first step would be to subtract 8 for both sides

Usually we stack these but here I am showing you a horizontal approach

8 + (-1)x -8  = 3- 8

(-1)x = -5

Divide each side by -1

(-1)x/-1 = -5/-1

x = 5

Method 2

Move the variable term to the right side FIRST!

8 = 3 + x

Now we need to subtract 3 from both sides

8 -3 = 3 + x – 3

5 = x

or x = 5

Solving a Two- Step Equation

Solve 3 -2x = 11

Again you can use either of the two different methods above.  With the second method, you move the variable over first to obtain a positive variable.

Method 1

3-2x = 11

You would subtract 3 from both sides

3 -2x -3 = 11-3

-2x = 8

Method 2

3-2x =11

3= 11+ 2x

-8 = 2x

 

-4 = x

Algebra Honors ( Periods 6 & 7)

Using Factoring to Solve Problems  5-13

Example 1

A decorator plans to place a rug in a 8 m by 12 m room so that a uniform strip of wood flooring around the rug will remain uncovered. How wide will this strip be if the area of the rug is to be half the area of the room?

Let x = the width of the strip

Then 12-2x is the length of the rug and 9 – 2x is the width of the rug

(12-2x)(9-2x) = the area of the rug.

Area of the rug = ½ ( area of the room)

(12-2x)(9-2x) = ½(9∙12)

108 – 42x + 4x² = 54

4x²- 42 + 108 = 54

4x²- 42 -54 = 0

2(2x²- 21 + 27) =0

2(2x -3)(x -9) = 0

using the ZERO Products Property

2x -3 = 0 or x= 3/2

x -9 = 0  x = 9

CHECK: x = 1.5

works but when x = 9

the length 12 – 2x and the width 9-2x are negative! Since a negative length or width is meaningless reject x = 9 as an answer

This show that also the equation has a root that does not check because this equation does not  meet the hidden requirements that the rug have a positive length.  

Example 2
The FORMULA h = rt – 4.9t² is a good approximation of the height (h) in meters of an object t seconds after it is projected upward with an initial speed of r meters per second.

An arrow is shot upward with an initial speed of 34.3 m/s. When will it be at a height of 49 m?

let t = the  number of seconds  after being shot that the arrow is 49 m high.

Let h = the height of the arrow= 49 m

Let r = the initial speed = 34.3 m/s

Substitute in the formula

h = rt – 4.9t²

49 = 34.3t – 4.9t²

4.9t² – 34.3t + 49 = 0  THINK—GCF???

4.9(t² – 7t + 10 ) = 0

4.9(t -2)(t -5) = 0

Using the ZERO PRODUCTS PROPERTY

t = 2 and t = 5

Therefore the arrow is 49 m high both 2 seconds and 5 seconds after being shot… on its way up and on its way down!

Example 3

If a number is added to its square, the results is 56. Find the number

 Let x = the number

x² + x = 56

(x +8)(x - 7) = 0

 x = -8 and x = 7

Find two consecutive positive odd integers whose product is 143

Let x = the first positive odd integer

Let x + 2 = the 2^nd positive odd integer

x(x + 2) = 143

x² + 2x = 143

x² + 2x – 143 = 0

(x + 13)(x – 11) = 0

x = -13 and x = 11

But ask only for the positive integers so reject -13

The two integers are 11 and  13

Example 4

The sum of the squares of two consecutive negative odd integers is 290. Find the integers

let x = the 1^st negative odd integer

let x + 2 = the 2^nd negative odd integer

x² + (x + 2)² = 290

x² + x² + 4x + 4 = 290

2x² + 4x – 286 = 0  THINK  GCF!!!

2(x²+ 2x -143) = 0

2(x + 13)(x -11) = 0

x = -13 and x = 11

But it ask for the negative integers  so reject x = 11

The two negative integers are -13 and -11

Math 6A ( Periods 1 & 2)

Least Common Multiple 5-6

Here is a review of that lesson...

Let’s look at the nonzero multiples of 8 and 12—listed in order

Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72…

Multiples of 12: 12, 24, 36, 48, 60, 72, ….

The numbers 24, 48, and 72, ... are called common multiples of 8 and 12. The least of these multiples is 24 and is therefore called the least common multiple.

LCM(8, 12) = 24

To find the LCM of two whole numbers, we can write out lists of multiples of the two numbers.

Or, we can use prime factorization

Lets find LCM(12, 15)

12 = 2²∙3

15 = 3∙5

The LCM will be made up of the greatest power of each factor

LCM will be 2²∙3∙5 = 60

The book has a third option or method

you can check out, if you’d like

Let’s find LCM (54, 60)

54= 2∙3∙3∙3 = 2∙3³

60 = 2∙2∙3∙5 = 2²∙3∙5

The greatest power of 2 that occurs in either prime factorization is 2²

The greatest power of 3 that occurs in either prime factorization is 3³

The greatest power of 5 that occurs in either prime factorization is 5

Therefore, LCM(54,60) is 2²∙3³∙5 = 540

REMEMBER:

The GCF (greatest common factor) is a factor. The GCF of two numbers will be either the smaller of the two or smaller than both

The LCM (least common multiple) is a multiple. The LCM of the two numbers will be the largest of the two or larger than both.

To find the LCM of two whole numbers you could write out the lists of multiples-- and that works relatively easily with small numbers... but there are more efficient ways to find the least common multiple of two whole numbers.

1. Write out the first few multiples of the larger of the two numbers and test each multiple for divisibility by the smaller number. The first multiple of the larger number that is divisible by the smaller number is the LCM

2. You can use prime factorization to find the LCM. The LCM is the PRODUCT OF EVERY factor to its GREATEST power!!

LCM(54, 60)

54 = 2⋅ 3⋅ 3⋅ 3 = 2⋅ 3³

60 = 2⋅ 2⋅ 3⋅ 5 = 2²⋅ 3⋅ 5

So the greatest power of 2 is 2²

The greatest power of 3 is just 3

and the greatest power of 5 is just 5

so the product of 2²⋅ 3⋅ 5 will be the LCM

LCM(54, 60) = 540

Second Day:

3. You may use the BOX method as shown in class... unfortunately it does not show well here. Remember you need to create a L The numbers on the side of the box represent the GCF!! You need to multiple them with the last row of factors.

See me before or after class if you want any review!!

We reviewed the concept of relatively prime and noticed that any two prime numbers are relatively prime. We also noticed that if two numbers are relatively prime-- neither of them must be prime....

We also found out that if one number is a factor of a second number, the GCF of the two numbers is the first number AND... if one whole number is a factor of a second whole number the LCM of the two numbers is the second number!!

GCF(12,24) = 12

LCM(12,24) = 24

WOW!!

If two whole numbers are relatively prime---

their GCF = 1

and their LCM is their product!!

GCF(8,9) =1

GCF(8,9) = 72

WOW!!

LCM & GCF Story Problems

1) Read the problem

2) Re-read the problem!!

3) Figure out what is being asked for!!

4) find the "magic " word... to help you determine if you are finding GCF or LCM

5) When in doubt... draw it out!!