Algebra Honors (Periods 6 & 7)

Complex Fractions Chapter 6 Extra 

A complex fraction is a fraction whose numerator or denominator  contains one or more fractions. To express a complex fraction as a simple faction use one of the following methods:

Method 1:  Simply the numerator and the denominator.  Express the fraction as a quotient using the division symbol  ÷ .   Multiply by the reciprocal of the divisor. 

Method 2: Find the LCD of ALL the simple fractions in the complex    fraction. Multiply the numerator and the denominator of the complex  fraction by the LCD 

Using Method 1

Method 1:  Simply the numerator and the denominator.  Express the fraction as a quotient using the division symbol  ÷ .   Multiply by the reciprocal of the divisor. 

Simplify above to get

Using Method 2

Method 2: Find the LCD of ALL the simple fractions in the complex    fraction. Multiply the numerator and the denominator of the complex  fraction by the LCD 

   

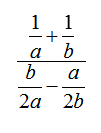
Same problem as above but this time Find the LCD of all the simple fractions in the complex fraction... The LCD would be 2ab. Multiply each simple fraction by 2ab

Which simplifies to

Then you can factor:

Hopefully you realize you have been able to obtain the same simplified fraction using EITHER method. Use whichever method works BEST for you!

Math 6A ( Periods 1 & 2)

Equations: All 4 Op’s

Review Sections 8-2 & 8-3

x = 48 + 15

There isn’t any transformations necessary

We just need to add the numbers on the right hadn side

x = 63

4( 3-1) + x = 34

4(2) + x = 34

8 + x = 34

subtract 8 from both sides

x = 26

Make sure to box your answers~

(Include the variable in your BOX!

n/16 = 6

We need to multiply both sides by 16

n = 96

17n = 289

Wait a minute… you should look at this and say… I know this one!

divide both sides by 17

n = 17

You know your squares and square roots!

YAY

Math 6A (Periods 1 & 2)

Equations: Decimals  8-4

You can use transformations to solve equations which involve decimals
Solve 0.42 x = 1.05
Divide both sides by 0.42
.42x/.42 = 1.05/.42
now, do side bar and actually divide carefully and you will arrive at
x = 2.5

1.6n = 3.6
1.6n/1.6 = 3.6/1.6
Carefully do the math and you find that
n = 2,25
If you need to-- practice with decimals! You need to be able to divide and multiply accurately!


Solve: n/.15 = 92
multiply both sides by .15 to undo the division
(n/.15)(.15) = 92 (.15)
Again, do a sidebar for your calculations and you will arrive at
n = 13.8


n + 0.519 = 0.597
we need to subtract 0.519 from both sides
n = 0.078

x - 0.323 = .873
we need to add 0.323 to both sides
x = 1.196


Reminder: the ultimate objective is applying transformations to an equation is to obtain an equivalent equation in the form x = c
(where c is a constant.)

Also remember that the understood (invisible) coefficient of x in the equation x = c is 1.

[Can you picture the poster in the front of the room?]