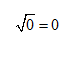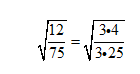Math 6A (Periods 2 &4)

Addition & Subtraction of Mixed Numbers 7-2

To add or subtract mixed numbers we could first change the mixed numbers to improper fractions and then use the method from 7-1 .
1 4/9 + 3 1/9 = 13/9 + 28/9 = 41/9 = 4 5/9 but that was 5th grade….
In the second method, and the one I prefer, you work separately with the fractional and whole number parts of the given mixed numbers.


STACK THEM!!
3 4/9
1 7/9
4 11/9 = 5 2/9


If the fractional parts of the given mixed numbers have different denominators, we find equivalent mixed numbers whose fractional parts have the same denominator, usually the LCD.

5 3/10 + 7 7/15

Stack

5 3/10
+7 7/15

Draw a line separating the fractional part from the whole numbers Find the LCM of the denominators the LCD and add…

9 5/9 - 4 13/15

Math 6A (Periods 2 & 4)

Addition and Subtraction of Fractions 7-1

Most of you already know how to add and subtract fractions, although some of you may need just a little review.

5/9 + 2/9 = 7/9
13/12 - 5/12 = 8/12 = 2/3
and that
7/9 – 2/9 = 5/9


13/12 - 5/12 = 8/12 = 2/3
a/c + b/c = (a +b)/c where c does not equal 0
a/c - b/c = (a -b)/c

The properties of addition and subtraction of whole numbers also apply to fractions.
If the denominators are the same— add or subtract the numerators AND use the numerator!!

In order to add two fractions with different denominators, we first find two fractions, with a common denominator, equivalent to the given fractions. Then add these two fractions.

The most convenient denominator to use as a common denominator is the least common denominator of LCD, of the two fractions. That is, the least common multiple of the two denominators.

LCD ( a/b, c/d) = LCM(b, d) where b and d both cannot be equal to 0

For example LCD ( 3/4, 5/6) = LCM(4,6) =12

3/4 = 9/12 and 5/6 = 10/12

Let’s do:
7/15 + 8/9

First find the LCD

LCM(15, 9) Do your factor trees or inverted division – or just by knowing!!

15 = 3• 5
9 = 3²

So LCM(15,9) = [every factor to its greatest power] 3²•5 = 45

Then find equivalent factions with a LCD of 45, and add

7/15 = 21/45

8/9 = 40/45

21/45 + 40/45 = 61/45 = 1 16/45

5/6- 11/24
Stack them and use the LCD
5/6 = 20/24
-11/24 = -11/24

9/24 = 3/8
7/12 + 4/9 + 3/4
several strategies ca be used. You can find the LCD for all three you can use the C+ and the A+
and change it to
(7/12 + 3/4) + 4/9
then add the first two factions
7/12 + 3/4 becomes 7/12 + 9/12 = 16/12 = 4/3
then add 4/3 + 4/9
change 4/3 to 12/9
12/9 + 4/9 = 16/9 = 1 7/9

What about 17/10 - ( 3/5 + 5/6)
You must do the parenthesis first
so 3/5 + 5/6
3/5 = 18/30
5/6 = 25/30
43/30
Now you have
17/10 - 43/30
stack those
17/10 = 51/30


51/30
^-43/30
8/30 = 4/15

Math 6High (Period 3)

Solving Addition Equations 5.3

Although you are very capable of doing many of these equations in your head, this lesson is about the process à rather than just getting the correct solution.

n + 8 = 17

The goal of solving equations is to isolate the variable on one side of the equation (all alone on one side of the equals sign)

To do that we use inverse operations. Inverse operations are operations that “undo” each other, such as addition and subtraction.

Subtraction Property of Equality

Subtracting the same number for EACH SIDE of an equation produces a new equation having the same solution as the original.

x + a = b  à x + a  - a = b -a

So  with n + 8 = 17

We need to isolate n from EVERYTHING else.

Since currently 8 is being added to our variable, we need to undo addition. The Inverse Operation we will use is subtraction. BUT, we need to subtract 8 from BOTH SIDES OF THE EQUATION.

Formal Check is easy:
Rewrite the equation first
Substitute in your solution for n  written in (hugs) Put a “?” over the equals sign at this point.
DO THE MATH… that is…   Make sure the left side = the right side

n  + 8 = 17

(9) + 8 = 17

17 = 17

What about the following

x + 9 = 4

To isolate the variable, we need to undo addition again. We need to subtract 9 from both sides of the equation.

x =  -

But wait!

Look at the right side of the equation now! We have different signs for Integers. We must follow the rules for Different Signs. First we determine who has the larger absolute value ( That’s our “who wins?”) We stack the winner on top. We know that our solutions MUST include a NEGATIVE. so let’s set up the solution with x = -    so we don’t forget.

Then after stacking the winner on top, we take the difference and discover that x = -5

FORMAL CHECK:

Rewrite the original equation
Substitute in our solution using (hugs)
DO THE MATH

x + 9 = 4

(-5) + 9  = 4

Use a side bar to check -5 + 9

We have different signs here as well. Who wins? The +9, by how much?

Stack them

so

x + 9 = 4

(-5) + 9 = 4

4 = 4

We did the following in class

n + 8 = -2

4 = x + 9

-12 = 11 + p

46 + b = -4

n + 7 = -7

You will be required to show all the balancing stepsà even f you could do these equations in your head.

You will also need to do a Formal Check for a few of the problems.

Algebra Honors (Period 5 & 6)

Rational Square Roots 11-3

You know that subtraction undoes addition, and that division by a nonzero number  undoes multiplication, Similarly squaring a number can be undone by finding a square root.

If a² =b     then a is a square root of b

Notice that 7²= 49 and so  does (-7)² = 49      So 7 and -7 are square roots of 49

the radical symbol √ is used to write the principal or positive square root of a positive number.

 is read    “The positive square root of 49 equals 7 

A negative square root is associated with the symbol     - √

is read “The negative square root of 49 equals -7”

Let’s use ± to indicate both the positive (also called the principal) square root and negative square root    so

 means the positive or negative square root  of 49     or   ±7

 Let’s look at      

   

the number written beneath the radical sign (such as 49) is called the radicand.

For all positive real numbers a:
Every positive real number a has two square roots    

The symbol  

                denotes the principal square root of a

Zero has only one square root—itself. 

             

Because the square of every real number is either positive or zero—>NEGATIVE NUMBERS DO NOT HAVE SQUARE ROOTS IN THE SET OF REAL NUMBERS.

 does not have a solution in the set of real numbers!!

Notice that

and that  

so...

Product Property of Square Roots
For any non-negative real numbers a and b,

Find: 

Let’s say you forgot your perfect squares—OH MY!!

but looking at 225, using your skills from previous years you realize 225 = 9 · 25  so

If you cannot see any perfect squares that divide the radicand—begin by factoring it!! Then see if you have any perfect squares.   USE INVERTED DIVISION!!

Always use PERFECT SQUARES when using inverted division. We practiced in class.

Use inverted division along with divisibility rules  to find perfect squares Look for the largest perfect square factors ...   and you discover that 

Quotient Property of Square Roots

For any non negative real number a and any positive real number:

Find the indicated square root

                                                                      

try:

 If you don’t see any perfect squares—especially with numbers like these—simplify your fraction first

sois really

and that's easy to do... it is  2/5

What about

Express as a decimal first then it should become easier

Let’s look at