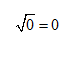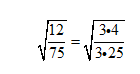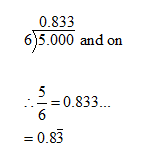Algebra Honors ( Periods 6 & 7)

Rational Square Roots 11-3

You know that subtraction undoes addition, and that division by a nonzero number  undoes multiplication, Similarly squaring a number can be undone by finding a square root.

If a² =b     then a is a square root of b

Notice that 7²= 49 and so  does (-7)² = 49      So 7 and -7 are square roots of 49

the radical symbol √ is used to write the principal or positive square root of a positive number.

 is read    “The positive square root of 49 equals 7 

A negative square root is associated with the symbol     - √

is read “The negative square root of 49 equals -7”

Let’s use ± to indicate both the positive (also called the principal) square root and negative square root    so

 means the positive or negative square root  of 49     or   ±7

 Let’s look at      

   

the number written beneath the radical sign (such as 49) is called the radicand.

For all positive real numbers a:
Every positive real number a has two square roots    

The symbol  

                denotes the principal square root of a

Zero has only one square root—itself. 

             

Because the square of every real number is either positive or zero—>NEGATIVE NUMBERS DO NOT HAVE SQUARE ROOTS IN THE SET OF REAL NUMBERS.

 does not have a solution in the set of real numbers!!

Notice that

and that  

so...

Product Property of Square RootsFor any non-negative real numbers a and b,

Find: 

Let’s say you forgot your perfect squares—OH MY!!

but looking at 225, using your skills from previous years you realize 225 = 9 · 25  so

If you cannot see any perfect squares that divide the radicand—begin by factoring it!! Then see if you have any perfect squares.   USE INVERTED DIVISION!!

Always use PERFECT SQUARES when using inverted division. We practiced in class.

Use inverted division along with divisibility rules  to find perfect squares Look for the largest perfect square factors ...   and you discover that 

Quotient Property of Square Roots

For any non negative real number a and any positive real number:

Find the indicated square root

                                                                      

try:

 2nd day:   If you don’t see any perfect squares—especially with numbers like these—simplify your fraction first

sois really

and that's easy to do... it is  2/5

What about

Express as a decimal first then it should become easier

Let’s look at

Algebra Honors ( Periods 6 & 7)

Decimal Forms of Rational Numbers 11-2

Any common fraction can be written as a decimal by dividing the numerator by the denominator. If the remainder is zero, the decimal is called a terminating, or ending, or finite decimal.

3/8=  0.375

Actually this is one of the fractions you need to know by heart !

If you don’t reach a remainder of zero when dividing the numerator by the denominator, continue to divide until the remainder begins to repeat.

5/6

  

7/11

The decimal quotient above are nonterminating,  nonending, or infinite. The dots indicate that the decimals continue without end.

They are also called repeating or periodic because the same digit or block of digits repeats unendingly. A bar (vinculum) is used to indicate the block of digits that repeat.

What ones do you need to know by heart… same from 6^th grade

1/3 family,   1/11 family,    and    let’s look at the 1/7 family (my favorite)

Let’s look at this algebraically… when you divide a positive integer n by a positive integer d, the remainder  r   at each step must be zero or a positive integer less than d.  For example, if the divisor is 6, the reminders will be 0, 1, 2, 3, 4, or 5 and the division will terminate or begin repeating within 5 steps after only zeros remain to be brought down.  Think about this!

For every integer   n and every positive integer   d, the decimal form of the rational number n/d either terminates or eventually repeats in a block of fewer than d digits.

To express a terminating decimal as a common fraction, express the decimal as a common fraction with a power of ten as the denominator. Then express in simplest form

                                                         

To express a repeating decimal follow these steps :  

Try it with  

You should get    179/330

How about     ? 

This one can be done easily if you remember the rule of matching the block of repeating digits with the digits in the decimal.

In this case        

All terminating and all repeating decimals represent rational numbers that can be written in the form n/d where n is an integer and d is a positive integer.

It is often convenient or even required that you use an approximation of a lengthy decimal. For example, you may approximate 7/13 as 0.53846, or 0.538, or 0.54       

As review: to round a decimal

1.       if the first digit dropped is greater than or equal to 5, add a 1 to the last digit retained.

2.       if the first digit dropped is less than 5, don’t change the last digit retained

Use the symbol    ≈   which means    “is approximately equal to”

Math 7 (Period 4)

Solving  Two Step Inequalities 9.8

Solving inequalities that require two or more steps—is very similar to solving equations

2x + 1 ≤4

subtract 1 from both sides

Divide both sides by 2

We then graphed this on a number line. We used a closed dot to indicate that 3/2 was part of the solution and our arrow went left. ( See page 484 Example 1)

Solve

We first added 5 to both sides

Now we need to multiply by -3 to both sides so as we do that operation, we must reverse the inequality symbol

m  < -21 

Math 6A (Periods 1 & 2)

Fractions 6-1

The symbol 1/4 can mean several things:
1) It means one divided by four
2) It represents one out of four equal parts
3) It is a number that has a position on a number line.

1/8 means 1 divided by 8 or 1 ÷ 8
A fraction consists of two numbers
The denominator tells the number of equal parts into which the whole has been divided.
The numerator tells how many of these parts are being considered.
we noted that we could abbreviate ...

denominator as
denom with a line above it

and numerator as numer

we found that you could add

1/3 + 1/3 + 1/3 = 3/3 = 1
or 1/4 + 1/4 + 1/4 + 1/4 = 4/4 = 1
we also noted that 8 X 1/8 = 8/8 = 1

We also noticed that 2/7 X 3 = 6/7


So we discussed the properties
For any whole numbers a, b,and c with b not equal to zero

1/b + 1/b + 1/b ... + 1/b = b/b = 1 for b numbers added together

and we noticed that b ∙  1/b = b/b = 1
we also noticed that

(a/b) ∙ c = ac/b

We talked about the parking lot problem on Page 180

A count of cars and trucks was taken at a parking lot on several different days. For each count, give the fraction of the total vehicles represented by
(a) cars
(b) trucks

Given: 8 cars and 7 trucks
We noticed that you needed to find the total vehicles or 8 + 7 = 15 vehicles

(a) fraction represented by cars is 8/15
(b) fraction represented by trucks is 7/15

What if the given was: 12 trucks and 15 cars

(a) fraction represented by cars is 15/27
(b) fraction represented by trucks is 12/27

What about
GIVEN:
9 cars and    35 vehicles
This time we need to find out how many trucks there are
35 - 9 = 26
so
(a) 9/35
(b) 26/35

We aren't simplifying YET

Algebra Honors ( Periods 6 & 7)

Properties of Rational Numbers 11-1

A real number that can be expressed as the quotient of two integers is called a rational number

A rational number can be written as a quotient of integers in an unlimited number of ways.

To determine which of two rational numbers is greater, you can write them with the same positive denominator and compare the numerators

Which is greater                                                           

?

the LCD is 21   

  

  

For all  integers  a and b and all positive integers c and d

   if an only if ad > bc

 if and only if ad < bc

This method compares the product of the extremes with the product of the means

Thus 4/7 > 3/8 because (4)(8) > (3)(7)

Rational Numbers differ from Integers in several ways. For example, given an integer, there IS a next greater integer.

That is, -8 is greater than -9. 1 follows 0, 35 follows 34 and so on. There is no “Next Greater” rational number after a given rational number.

The Density Property for Rational Numbers
Between every pair of different rational numbers there is another rational number

The density property implies that it is possible to find an unlimited or endless number of rational numbers between two given rational numbers.

If a and b are rational numbers and a < b  then the number halfway from a to b is

 and the number one third of the way from a to b would be

and so on.