Math 6A( Periods 1 & 2)

Rates 5-3

A RATE is a ratio of two quantities using different units!  

A UNIT RATE compares a quantity to one unit of another quantity

For example, you pay $27 for 3 pizzas.  The UNIT RATE is $ 9 : 1 pizza

Notice there are LABELS!  LABELS are essential when describing all rates!

Some well know unit rates: Miles Per Hour (MPH, Miles Per Gallon ( MPG), Revolutions Per Minute (RPM) or Revolutions Per Second ( RPS) and  Heartbeats per minute. Do you know any?

 Equivalent rates have the same  UNIT RATE

Rate  a units: b units     Unit Rate: a units : 1 unit
                                    b

A double number line can show the rate at which you earn points for hitting notes in a music video game.  Write a rate that represents this situation.

Rate: 600 points for 4 notes or 300 points for 2 notes or 450 points for 3 notes or 750 points for 5 notes.

150 points for every note would be the unit rate!

Finding UNIT RATE

A piece of space junk travels 5 miles in 8 seconds. How far does it travel per second?

You can set up a Ratio table to see

Distance ( mi)	5	5/8
Time ( seconds)	8	1

          

It travels 5/8 mile PER second

Notice the TIME must be 1 second!

Japanese Bullet Train traveled 558 miles in 3 hours. How far did it travel every hour?

Again, you can set up the RATIO Table

Distance ( miles)	558	558/3
Time ( Hours)	3	1

 Really do the division, carefully!                                                                             

Did you check to see if it was divisible by 3—BEFORE you began?

Chef has 6 pounds of salmon fillet for $51.00. How much will the chef pay for 9 MORE pounds of salmon?

Think: Will UNIT RATE help me find the solutions?

Cost $	51	8.50	76.50
Salmon ( lb)	6	1	9

 $76.50 for 9 more pounds of salmon
Show your division     What is the next step here:   

Could you have done it a different way?  Hmmm… 51 and 6 are both divisible by 3. Would that help?

Cost $	51	25.50	76.50
Salmon ( lb)	6	3	9

   SAME Result:  $76.50 for 9 more pounds of salmon     

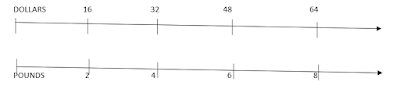
Two pounds of Ahi for $ 16.00 What is the cost for 7 lbs of Ahi?

Because 16 is easily divided into pieces, you might want to use a double number line

                        

Several ways to think about this problem! Unit rate is just one of them!

7 is halfway between 6 and 8 (You can visualize that with the number line) … so What value is halfway between 48 and 64?      

The cost is $56.00 for 7 pounds of Ahi.

Math 6A ( Periods 1 & 2)

Ratio Tables 5-2

Essential Question:  How can you find two ratios that describe the same relationship?

We looked at a recipe or mixture of lemonade and iced tea.

the one from the book called for 1 cup of lemonade for every 3 cups of iced tea

We created a table and thought of various combinations that still kept that same relationship

C. of Lemonade	1	2	3	5	8	10
C. of Iced tea	3	6	9	15	24	30
Total Cups	4	8	12	20	32	40

A mixture contains 13 cups of lemonade, how could we determine how many cups of iced tea would be required? How could we use the given table to find that answer? 
1) we saw that the relationship was 1:3 so we could multiply 3 (cups of iced tea) by 13 to get 39 cups of iced tea.
2) we could use the existing information in the table. We know that 5 + 8 = 13 so if we just add the information for iced tea in those columns ( 15 + 24 =39) we would get 39 cups of iced tea as well.

Two ratios that describe the same relationship are equivalent ratios. You can find equivalent ratios by:

·        adding or subtracting quantities in equivalent ratios

·        multiplying or dividing each quantity in a ratio by the same number.

You can find and organize ratios in a ratio table.

Pens	1	2
Pencils	3		9

using repeated addition:

Pens	1	2	3
Pencils	3	6	9

The equivalent ratios are 1:3; 2:6 and 3:9

Dogs	4		24
Cats	6	12

You can use multiplication to find the missing values

Dogs	4	8	24
Cats	6	12	36

The equivalent ratios are 4:6; 8:12 and 24:36

We discussed how they are all equivalent to 2:3 as well

Using a Ratio Table in a word problem

The nutrition fact labeled on a box of crackers shows that there are 240 milligrams of sodium in every 36 crackers.

You eat 15 crackers. How much sodium do you consume?

The ratio of sodium to crackers is 240 to 36. Create a ratio table to find equivalent ratios with 15 crackers.

Sodium (mg)	240	120	20	100
Crackers	36	18	3	15

The ratio 100 to 15 is equivalent to 240 to 36.

So, you consumed 100 milligrams of sodium.

You eat 21 crackers. How much sodium do you consume?

Notice, you can add the two middle columns in the table above to find the solution to that question.

Since 18 + 3 = 21 120 + 20 = 140   140 milligrams of sodium in in 21 crackers.
You could also use the ratio 20:3 and multiply both by 7 and you will arrive at 140:21 or 140 milligrams of sodium