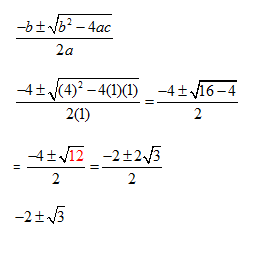Pi Day, March 14, 2013

HAPPY PI DAY


HAPPY PI DAY! WHAT AN IRRATIONAL DAY!!!!
BE IRRATIONAL.. AND TRANSCENDENTAL
... here are the facts:
Today we celebrate Π (Pi), a very cool number. Π is a comparison between the measurements of the circumference to the diameter of a circle—any circle.
Pi is an IRRATIONAL number. That means it has no pattern and never terminates.
It CANNOT be written as a fraction with an integer in the numerator and denominator.

We use 3.14 and 22/7 as APPROXIMATIONS of pi.

These are not the exact values. The only symbol that tells the exact value is Π. Pi is a ratio, a comparison between two numbers.

You will be able to discover many interesting facts about pi—even finding it on your own.

Here's some links to click on if you're interested in the mystery of Pi:




History of pi
Find your birthday in pi
The first ten thousand digits of pi


Here is a rap I really like...


Lose Yourself in the Digits of pi


... and of course... here are the songs we sang

Happy Pi Day (to the tune of “Happy Birthday”)

Happy PI day to you
Happy PI day to you
Happy PI day everybody
Happy PI day to you



Oh, Number Pi (to the tune of “Oh, Christmas Tree”)

Oh, Number Pi
Oh, Number Pi
Your digits are unending.
Oh Number Pi
Oh Number Pi
No pattern are you sending
You’re three point one four one five nine
And even more if we had time,
Oh, number Pi
Oh, number Pi
For circle lengths unbending.

Oh, number Pi
Oh, number Pi
You are a number very sweet
Oh, number Pi
Oh, number Pi
Your uses are so very neat.
There’s 2 Pi r and Pi r squared
A half a circle and you’re there,
Oh, number Pi
Oh, number Pi
We know that Pi’s a tasty treat




Pi Day Song (to the tune of “Jingle Bells”)

Pi day songs
All day long
Oh what fun it is
To sing a jolly pi day song
In a fun math class
Like this

Verse;
Circles in the snow
Around and round we go
How far did we have to run?
Diameter times pi! (Refrain)

We wish you a Happy Pi Day (to the tune of “We wish you a Merry Xmas”)

We wish you a happy Pi Day
We wish you a happy Pi Day
We wish you a happy Pi Day
To you and to all

Pi numbers for you
For you and for all
Pi numbers in the month of March
So three point one four!!

Algebra Honors ( Periods 5 & 6)

 Graphs of Quadratic Equations: The Discriminant  12-4

Sometimes it is NOT necessary to draw the graph of an equation.
Knowing the relationships between an equation and its graph— you can obtain important information from the equation itself.

Today’s lesson illustrates the relationship between the number of roots of a quadratic equation and the number of x-intercepts of the related parabola.

In the parabola the x coordinate of a point where the curve intersects the x axis is called an x-intercept of the curve.

Looking at the parabola on page 572 you notice that this parabola has two x-intercepts, -1 and 3 because y = 0 for both of these values of x.

you can also see that
x²- 2x – 3 = 0 or (x +1)(x-3) = 0

has -1 and 3 as its roots, solutions, zeros… {-1,3}

The algebraic fact that a quadratic equation can have two, one or no real number roots corresponds to the fact that a parabola can have two, one or no x-intercepts…

and we can find that out by just working with the quadratic equations—rather than having to graph…

However… let’s graph a few
Example 1: x² + 4x + 1 = 0
find –b/2a
-4/2 = -2
f(-2) = (-2)² + 4(-2) + 1 = 4 -8 + 1 = -3
so (-2,-3) is the vertex

x = -2 is the axis of symmetry

Create an x y table

f(-1) = (-1)² +4(-1) + 1 = 1 -4 +1 = -2
f(0) = 02 + 4(0) + 1 = 1
x y
-1 -2
0 1

Now solve
Solving x² + 4x + 1 = 0

Now graph
Number of roots: two real roots Number of x-intercepts: two


Example 2 : x² + 2x + 1 = 0

find -b/2a -2/2 = -1
f(-1) = (-1)² + 2(-1) + 1 = 1 -2 + 1 = 0

(-1.0) is the vertex

and x = -1 is the axis of symmetry
create an xy table
f(0)=0² + 2(0) + 1 = 1
f(1) = (1)² +2(1) + 1 = 4
x y
0 1
1 4
Now graph


Now Solve
Solving x² + 2x + 1 = 0
We can solve easily but let’s use the quadratic formula

= -1






The solution set is {-1}

Number of roots: 1 real root Number of x- intercepts: one

Example 3: x² -4x + 7 = 0

find –b/2a=        +4/2 = 2
f(2) = (2)² -4(2) + 7 = 4 -8 + 7 = 3

vertex ( 2, 3)
and x= 2 is the axis of symmetry

create an xy table
f(1) = (1)² -4(1) + 7
f(0) = (0)² -4(0) + 7
x y
1 4
0 7
Now graph
Now solve
x² -4x + 7 = 0

There is NO REAL number root since does not represent a real number

Number of roots: no real number roots Number of x intercepts: None


In each of these examples the value of b²-4ac in the quadratic formula is the key to the number of real roots.

When b²-4ac is negative, there is no real number root of the equation ax² + bx + c = 0 because square roots of negative numbers do not exist in the set of real numbers.

Because the value of b²-4ac discriminates, or points out differences, among these 3 cases above, it is called the discriminant of the quadratic equation.

The discriminant is only part of the quadratic formula and simpliy helps one determine the number of roots.

If  b²-4ac <  0 "no real roots"
If  b²-4ac =  0 "one rational root"
If  b²-4ac  >   0 " two real roots"  we can break this down even more specific:

If  b²-4ac  is a perfect square then " two rational roots"
If  b²-4ac  is a non-square then  "two  irrational roots"

Algebra Honors (Period 6 & 7)

 The Quadratic Formula 12-3

Make sure to read the first post on the Quadratic Formula BEFORE or AFTER you watch these You Tube Videos....

How about creating your own video!! (For extra Credit!!)

Now if Emily can recite the Quadratic Formula after singing Twinkle, Twinkle Little Star... shouldn't you?

Math 6A (Periods 2 & 4)

Subtracting Integers 11-3

The life story about someone who was so negative-- you wanted to take a little negativity away but since you can't do that you add a little positiveness-- works in math as well!!
Instead of subtracting ... "ADD THE OPPOSITE!"
We proved it in class with our little red and yellow tiles... If you need to review, make your own out of red and yellow paper-- or whatever colors you want!!

In life-- to take away a little negative-- add some positive

To take away an integer... add its opposite.

Rule from our textbook
for all integers a and b

a - b = a + (the opposite of b) or
a - b = a + (-b)

Instead of subtracting.. "ADD THE OPPOSITE"
make sure you do the check, check.. you need to have two check marks.. one changing the subtraction to addition and the other changing the sign of the 2nd number to its opposite.

5 - ^- 2=
5 + ⁺ 2= 7

-2 - 5 =
- 2 + ^- 5 =
before I give you the answer look... we are looking at
-2 + ^-5
We are adding two negatives.. so we are back to the rules from Section 11-2...
when adding the same sign just add the number and use their sign so
- 2 + ^- 5 = -7

But what about -2 - ^-5 ?
adding the opposite, we get
-2 + ⁺ 5 .
Now, the signs are different so the rule from Section 11-2 is
ask yourself... "Who wins?" and "By how much?"

Okay, here the positive wins so I know the answer will be +
and by how much means.. to take the difference
5-2 = 3
so -2 + ⁺ 5 = +3
Do you need to put the + sign? No, but I like to in the beginning to show that I checked WHO WON!!

What about
-120 - ^-48?
add the opposite
-120 + ⁺ 48 follows the
Different signs rule... so
ask yourself
Who wins? answer: the negative.. so I know the answer will be negative..
And "By How Much?" take the difference 120-48 = 72
so
-120 + ⁺ 48 = -72
or

-120 - 48
-120 + (-48) = -168

NEVER EVER CHANGE THE FIRST NUMBER'S SIGN!!

WALK THE LINE, the number line-- that is!!
Remember... Attitude is such a little thing... but it makes a BIG difference!!
Always start with a positive attitude!!
When you walk the line, Which way are you always facing when you start???

Always attempt to get everything into addition so we can follow the rules of Section 11-2 Adding Integers.
1) SAME SIGN rule---> just add the numbers and use their sign
-4 + -5 = -9
2) DIFFERENT SIGNS rule
ask yourself those 2 important questions
a) Who wins? (answer is either negative or positive)
b) By how much? (Take the difference)

Page 376 answers to # 2-18 (evens)
2. -9
4. -5
6. 22
8. -9
10. -74
12. -32
14. -160
16. 498
18. -284

Algebra Honors (Periods 5 & 6)

The Quadratic Formula: 12-3

Method 5:
THE QUADRATIC FORMULA

Let's all sing it to "Pop Goes the Weasel!

"
x = -b plus or minus the square root of b squared minus 4ac all over 2a

x =
-b ± √ (b² - 4ac)
2a

Notice how the first part is the x value of the vertex -b/2a


The plus or minus square root of b squared minus 4ac represents 
how far away the two x intercepts (or roots) are from the vertex!!!!



Very few real world quadratics can be solved by factoring or square rooting each side.


And completing the square always works, but it long and cumbersome!

All quadratics can be solved by using the QUADRATIC FORMULA.

You will find out that some quadratics have NO REAL solutions, which means that there are no x intercepts - the parabola does not cross the x axis!
Think about what kinds of parabolas would do this....ones that are smiles that have a vertex above the x or ones that are frowns that have a vertex below the x axis.
You will find out in Algebra II that these parabolas have IMAGINARY roots




So now you know 5 ways that you know to find the roots:


1. graph


2. factor if possible


3. square root each side


4. complete the square - that's what the quadratic formula is based on!


5. plug and chug in the Quadratic Formula -
This method always works if there's a REAL solution!




DON'T FORGET TO PUT THE QUADRATIC IN STANDARD FORM BEFORE PLUGGING THE VALUES INTO THE QUADRATIC FORMULA!


You should know that for the quadratic formula, you don't need the "a" coefficient to be positive!

That's important if you use factoring, SQRTing each side, and completing the square.


But for the quadratic formula, either way, you'll get the same roots!


EXAMPLE: x² + 8x = 48 


You can move the 48 over or move the x² + 8x over and you'll get the same answers!
Let's look at:


"a" coefficient positive *****vs***** "a" coefficient negative



x² + 8x - 48 = 0 ****VS**** -x² - 8x + 48 = 0


First x² + 8x - 48 = 0
-8 ± √[64 - 4(1)(-48)]

2(1)



-8 ± √(64 + 192)

2



-8 ± √(256)
2



-8 ± 16
2



(-8 + 16)/2 and (-8 - 16)/2



8/2 and -24/2
4 and -12

Now let's compare -x² - 8x + 48 = 0


8 ± √[64 - 4(-1)(48)]

-2(1)

8 ± √(64 + 192)

-2

8 ± √(256)
-2


8 ± 16
-2

(8 + 16)/-2 and (8 - 16)/-2
24/-2 and -8/-2
-12 and 4

So all the signs are simply the opposite of each other and therefore the answers are the same

Math 6A (Periods 2 & 4)

Adding Integers 11-2

Rules: The sum of two positive integers is a positive integer.
The sum of two negative integers is a negative integer.

So- if the two numbers have the same sign, use their sign and just add the numbers.

-15 + -13 = - 28

-10 + -4 = -14

Rules: The sum of a positive integer and a negative integer is :

POSITIVE… IF the positive number has a greater absolute value

NEGATIVE… IF the negative number has a greater absolute value

ZERO… IF both numbers have the same absolute value

Think of a game between two teams- The POSITIVE TEAM and The NEGATIVE TEAM.

30 + -16 … ask yourself the all important question…
“WHO WINS?
in this case the positive and then ask
“BY HOW MUCH?”
take the difference 14

14 + - 52…
“WHO WINS?”
the negative… “BY HOW MUCH?”
38
so the answer is -38


(-2 + 3) + - 6 you can work this 2 ways

(-2 + 3) + - 6 = 1 + -6 = -5 or
using all the properties that work for whole numbers
Commutative and Associative properties of addition
can change expression to (-2 + -6) + 3 or -8 + 3 = -5 you still arrive at the same solution.

You want to use these properties when you are adding more than 2 integers.
First look for zero pairs—you can cross them out right away!!
3 + (-3) = 0
-9 + 9 = 0

Then you can use C(+) to move the integers around to make it easier to add them together rather than adding them in the original order. In addition, you can use A(+) to group your positive and negative numbers in ways that make it easier to add as well.

One surefire way is to add all the positives up… and then add all the negatives up.
At this point ask yourself that all important question… WHO WINS? …
use the winner’s sign..
and then ask yourself..
BY HOW MUCH?

example:

-4 + 27 +(-6) + 5 + (-4) + (6) + (-27) + 13

Taking a good scan of the numbers, do you see any zero pairs?
YES—so cross them out and you are left with
-4 + 5 + (-4) + 13
add your positives 5 + 13 = 18
add your negatives and use their sign – 4 + -4 = -8

Okay, Who wins? the positive
By how much? 10
so
-4 + 27 +(-6) + 5 + (-4) + (6) + (-27) + 13 = 10

Algebra Honors (Periods 5 & 6)

Completing the Square: 12-2
METHOD 4:


Now this is completely new to you!!!

When does the square root = ± square root method work well?

When the side with the variable is a PERFECT SQUARE! We saw that in the previous section.
perfect square = k ( when k ≥ 0)

So what if that side is not a perfect BINOMIAL SQUARED?

It may be possible to trasform it into one... by COMPLETING THE SQUARE
You can follow steps to make it into one!

Why is this good? 

Because then you can just square root each side to find the roots!


THIS METHOD ALWAYS WORKS!


EXAMPLE:
x² - 3x -18 = 0

(Head's up-- I wouldn't use this method here because I can see that it factors easily... into (x-6)(x+3) = 0 so the solution set is {-3,6}
However, knowing what I need to get for my solutions might be a good way to practice Completing the square..
so

x² - 3x = 18

Step 1) b/2

That is, take half of the b coefficient ,
or in this case (- 3/2)



Step 2) Square b/2

(b/2)²
(-3/2 ⋅ -3/2 = 9/4)


Step 3) Add (b/2)² to both sides of the equation

x² - 3x + 9/4 = 18 +9/4

Step 4) Factor to a binomial square

(x - 3/2)² = 18 + 9/4
 = 81/4


Step 5) Square root each side and solve

√(x - 3/2)² = √ 81/4

x - 3/2 = ± 9/2
x = 3/2 ± 9/2
x = 3/2 + 9/2 AND x = 3/2 - 9/2
x = 6 and x = -3
{-3, 6}
We got the same solutions !! Yay!!


x² - 10x = 0


Not a TRINOMIAL SQUARE so it would not factor to a BINOMIAL SQUARED.

But here's how you can make it one!


Step 1) b/2

That is, take half of the b coefficient ,
or in this case (- 10/2 = -5)


Step 2) Square b/2

(b/2)²
(-5 x -5 = 25)

Step 3) Add (b/2)² to both sides of the equation

x² - 10x + 25 = +25
Step 4) Factor to a binomial square

(x - 5)² = 25

Step 5) Square root each side and solve

√(x - 5)² = √ 25

x - 5 = ± 5

Step 6) ADD 5 TO BOTH SIDES

x - 5 = ± 5
+ 5 = +5
x = 5 ± 5
Step 7) Simplify if possible

x = 5 + 5 and x = 5 - 5

x = 10 and x = 0



So the 2 roots (solutions/zeros/x intercepts) are 0 and 10.
YOU DON'T NEED TO GRAPH THE PARABOLA, BUT IF YOU DID, IT WOULD CROSS THE X AXIS AT 0 AND 10.
I don't know where the vertex is, but I don't need to because it's not the solution to the quadratic (although I certainly could find the vertex by using x = -b/2a)
Notice that I could also factor x² - 10x = 0 to get the solution more easily.
So don't complete the square if the quadratic factors easily!

IF THERE IS A "c", first move the c constant to the other side of the equation before completing the square:
x² - 10x - 11 = 0
x² - 10x - 11 + 11 = 0 + 11
x² - 10x = 11
NOW COMPLETE THE SQUARE AS ABOVE:
x² - 10x + 25 = +25 + 11
(x - 5)² = 36
√ (x - 5)² = √ 36
x - 5 = ± 6
x = 5 ± 6
x = 11 and x = -1

Again, this one factored easily so I wouldn't have even used completing the square. ALWAYS CHECK IF IT FACTORS FIRST!
Now an example that DOES NOT FACTOR: x² - 10x - 18 = 0
x² - 10x - 18 = 0
x² - 10x - 11 + 18 = 0 + 18
x² - 10x = 18
NOW COMPLETE THE SQUARE AS ABOVE:
x² - 10x + 25 = +25 + 18
(x - 5)² = 43
√ (x - 5)² = √ 43
x - 5 = ± √ 43
x = 5 ± √ 43
x = 5 + √ 43 and x = 5 - √ 43
When there is an IRRATIONAL square root, always SIMPLIFY if possible!

IF THERE IS AN "a" COEFFICIENT, YOU MUST DIVIDE EACH TERM BY IT BEFORE YOU CAN COMPLETE THE SQUARE:

Example: 2x² - 3x - 1 = 0
Move the 1 to the other side of the equation:
2x² - 3x = 1

Divide each term by the "a" coefficient:

x² - 3/2 x = 1/2

Now find the completing the square term and add it to both sides:
[(-3/2)(-3/2)]2 = 9/16
x² - 3/2 x + 9/16 = 1/2 + 9/16

(x - 3/4)² =8/16 + 9/16

(x - 3/4)² = 17/16
√[(x - 3/4)² ] = ±√ [17/16]

x - 3/4 = ±[√17] /4

x = 3/4 ±[√ 17] /4

x = (3 ± [√17]) /4
or written better x =
3 ± √ 17
4

Math 6A (Periods 2 & 4)

Negative Numbers 11-1

On a horizontal number line we use negative numbers for the coordinates of points to the left of zero. We denote the number called ‘negative four’ by the symbol -4. The symbol -4 is normally read ‘ negative 4’ but we can also say ‘ the opposite of 4.’

The graphs of 4 and -4 are the same distance from 0—>but in opposite directions. Thus they are opposites. -4 is the opposite of 4.

The opposite of 0 is 0

Absolute Value is a distance concept. Absolute value is the graph of the distance of a number from 0 on a number line. The absolute value of a number can NEVER be negative!!

Counting (also known as Natural) numbers: 1, 2, 3, 4, ….
Whole numbers 0, 1, 2, 3, 4….
Integers are natural numbers and their opposites AND zero
…-4, -3, -2, -1, 0, 1, 2, 3, 4….

The opposite of 0 is 0.

The integer 0 is neither positive nor negative.

The farther we go to the right on a number line--- the bigger the number. We can compare two integers by looking at their position on a number line.

if x < 0 what do we know? x is negative number if x > 0, what do we know? x is a positive number

We have been practicing representing integers by their graphs, that is, by points on a number line.

Make sure that your number line includes arrows at both ends and a line indicating where zero falls on your number line.
The graph of a number MUST have a closed dot right on the number line at that specific number.
Please see our textbook page 366 for an accurate example.