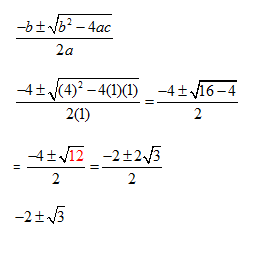Solving Problems Involving Quadratic Equations 12-6
You can use quadratic equations to solve problems...
We used the examples in the book to start with:

The park commission wants a new recantangluar sign with an area of 25 m² for the visitor center. The lenthght of the sign is to be 4 m longer than the width . To the nearest tenth of a meter, what wil be the length and the width of the sign?
Always make sure you check before AND after-- to see wht the problem is really asking for...
Let x = the width in meters
then x + 4 = the length in meters

Use the formula for the area of a recntagle to write an exquation

x(x+4) = 25
solve it
x(x +4) = 25 becomes
x² + 4x = 25
You can use two methods: the quadratic formula would be my second choice since completing the square works easily here

x² + 4x + 4 = 25 + 4
(x + 2)² = 29
x + 2 = ±√29
You can use your calculator, or the table of square roots... or approximately easily using the method taught in class earlier this year
but to the nearest tenth you get
-2 + √29 ≈3.4
-2 - √29 ≈-7.4

Since you can't have a negative root since a negative length has no meaning... you know the width must be about 3.4 meters and therefore the length is 3.4 +4 or approximately 7.4 meters

Problem 2:
The sum of a number and its square is 156. Find the number

Let x = the number
then
x² + x = 156

x² + x - 156 =0
Using the skills you have for factoring
(x +13)(x-12) = 0
so
x = 13 and x = 12
You have two solutions to this question!!

Problem 3:
The altitude of a triangle is 9 cm less than the base. The area is 143 cm²
What are the altitude and base?

Remember the formula for the area of a triangle is A = ½bh

Let b = the length of the base
then the altitude ( the height) is b-9
so
½(b)(b-9) = 143
b² -9b = 286
b² -9b - 286 = 0
(b -22)(b +13) = 0
b = 22 and b= -13
You can't have a negative length so
the base is 22 cm and the altitude is 13 cm


An object that moves through the air and is solely under the influence of gravity is called a projectile. The approximate height (h) in meters of a projectile at t seconds after it begins its flight from the ground with initial upward velocity v₀ is given by the formula
h = -5t² + v₀t
We can find when such a projectile is at ground level (h=0) by solving
0 = -5t² + v₀t.
If a projectile begins its flight at height c, its approximate height at time t is
h = -5t² + v₀t + c .
We can find when it hits the ground by solving h=0 or
0 = -5t² + v₀t +c.

When a projectile is thrown into the air with an initial vertical velocity of r feet per second, its distance (d) in feet above the starting point t seconds after it is thrown is approximately
d = rt – 16t²

Math 6 Honors ( Periods 1, 2, & 3)

Subtracting Integers 11-3

The life story about someone who was so negative-- you wanted to take a little negativity away but since you can't do that you add a little positiveness-- works in math as well!!
Instead of subtracting ... "ADD THE OPPOSITE!"
We proved it in class with our little red and yellow tiles... If you need to review, make your own out of red and yellow paper-- or whatever colors you want!!

In life-- to take away a little negative-- add some positive

To take away an integer... add its opposite.

Rule from our textbook
for all integers a and b

a - b = a + (the opposite of b) or
a - b = a + (-b)

Instead of subtracting.. "ADD THE OPPOSITE"
make sure you do the check, check.. you need to have two check marks.. one changing the subtraction to addition and the other changing the sign of the 2nd number to its opposite.

5 - ^- 2=
5 + ⁺ 2= 7

-2 - 5 =
- 2 + ^- 5 =
before I give you the answer look... we are looking at
-2 + ^-5
We are adding two negatives.. so we are back to the rules from Section 11-2...
when adding the same sign just add the number and use their sign so
- 2 + ^- 5 = -7

But what about -2 - ^-5 ?
adding the opposite, we get
-2 + ⁺ 5 .
Now, the signs are different so the rule from Section 11-2 is
ask yourself... "Who wins?" and "By how much?"

Okay, here the positive wins so I know the answer will be +
and by how much means.. to take the difference
5-2 = 3
so -2 + ⁺ 5 = +3
Do you need to put the + sign? No, but I like to in the beginning to show that I checked WHO WON!!

What about
-120 - ^-48?
add the opposite
-120 + ⁺ 48 follows the
Different signs rule... so
ask yourself
Who wins? answer: the negative.. so I know the answer will be negative..
And "By How Much?" take the difference 120-48 = 72
so
-120 + ⁺ 48 = -72

NEVER EVER CHANGE THE FIRST NUMBER'S SIGN!!

WALK THE LINE, the number line-- that is!!
Remember... Attitude is such a little thing... but it makes a BIG difference!!
Always start with a positive attitude!!
When you walk the line, Which way are you always facing when you start???

Always attempt to get everything into addition so we can follow the rules of Section 11-2 Adding Integers.
1) SAME SIGN rule---> just add the numbers and use their sign
-4 + -5 = -9
2) DIFFERENT SIGNS rule
ask yourself those 2 important questions
a) Who wins? (answer is either negative or positive)
b) By how much? (Take the difference)

Page 376 answers to # 2-18 (evens)
2. -9
4. -5
6. 22
8. -9
10. -74
12. -32
14. -160
16. 498
18. -284

Math 6 Honors ( Periods 1, 2, & 3)

Adding Integers 11-2

Rules: The sum of two positive integers is a positive integer.
The sum of two negative integers is a negative integer.

So- if the two numbers have the same sign, use their sign and just add the numbers.

-15 + -13 = - 28

-10 + -4 = -14

Rules: The sum of a positive integer and a negative integer is :

POSITIVE… IF the positive number has a greater absolute value

NEGATIVE… IF the negative number has a greater absolute value

ZERO… IF both numbers have the same absolute value

Think of a game between two teams- The POSITIVE TEAM and The NEGATIVE TEAM.

30 + -16 … ask yourself the all important question…
“WHO WINS?
in this case the positive and then ask
“BY HOW MUCH?”
take the difference 14

14 + - 52…
“WHO WINS?”
the negative… “BY HOW MUCH?”
38
so the answer is -38


(-2 + 3) + - 6 you can work this 2 ways

(-2 + 3) + - 6 = 1 + -6 = -5 or
using all the properties that work for whole numbers
Commutative and Associative properties of addition
can change expression to (-2 + -6) + 3 or -8 + 3 = -5 you still arrive at the same solution.

You want to use these properties when you are adding more than 2 integers.
First look for zero pairs—you can cross them out right away!!
3 + (-3) = 0
-9 + 9 = 0

Then you can use C(+) to move the integers around to make it easier to add them together rather than adding them in the original order. In addition, you can use A(+) to group your positive and negative numbers in ways that make it easier to add as well.

One surefire way is to add all the positives up… and then add all the negatives up.
At this point ask yourself that all important question… WHO WINS? …
use the winner’s sign..
and then ask yourself..
BY HOW MUCH?

example:

-4 + 27 +(-6) + 5 + (-4) + (6) + (-27) + 13

Taking a good scan of the numbers, do you see any zero pairs?
YES—so cross them out and you are left with
-4 + 5 + (-4) + 13
add your positives 5 + 13 = 18
add your negatives and use their sign – 4 + -4 = -8

Okay, Who wins? the positive
By how much? 10
so
-4 + 27 +(-6) + 5 + (-4) + (6) + (-27) + 13 = 10

Algebra Honors (Period 6 & 7)

Methods of Solutions 12-5
You have learned four different methods of solving quadratics.. picking the best one is the challenge
Here are some tips on when to use each method:
Quadratic Formula--> when to use: ax² +bx + c = 0 (It always works) Great when you have a calculator

Factoring--> when to use: ax² +bx + c = 0 you see the factors easily or you have ax² +bx = 0

Using the Property of SQRT's --> when to use: ax² + c = 0

Completing the square --> when to use: x² +bx + c = 0 especially when b is even

Which method would you use for the following?
x² +5x - 6 = 0
Answer: Factoring
x² -2x = 1
Answer: Completing the square
11x² = 44
Answer: SQRTing
3x² -5x = 4
Answer: Quadratic Formula

Algebra Honors (Period 6 & 7)

Graphs of Quadratic Equations:The Discriminant 12-4

Sometimes it is NOT necessary to draw the graph of an equation.
Knowing the relationships between an equation and its graph— you can obtain important information from the equation itself.

Today’s lesson illustrates the relationship between the number of roots of a quadratic equation and the number of x-intercepts of the related parabola.

In the parabola the x coordinate of a point where the curve intersects the x axis is called an x-intercept of the curve.

Looking at the parabola on page 572 you notice that this parabola has two x-intercepts, -1 and 3 because y = 0 for both of these values of x.

you can also see that
x²- 2x – 3 = 0 or (x +1)(x-3) = 0

has -1 and 3 as its roots, solutions, zeros… {-1,3}

The algebraic fact that a quadratic equation can have two, one or no real number roots corresponds to the fact that a parabola can have two, one or no x-intercepts…

and we can find that out by just working with the quadratic equations—rather than having to graph…

However… let’s graph a few
Example 1: x² + 4x + 1 = 0
find –b/2a
-4/2 = -2
f(-2) = (-2)² + 4(-2) + 1 = 4 -8 + 1 = -3
so (-2,-3) is the vertex

x = -2 is the axis of symmetry

Create an x y table

f(-1) = (-1)² +4(-1) + 1 = 1 -4 +1 = -2
f(0) = 02 + 4(0) + 1 = 1
x y
-1 -2
0 1

Now solve
Solving x² + 4x + 1 = 0

Now graph
Number of roots: two real roots Number of x-intercepts: two


Example 2 : x² + 2x + 1 = 0

find -b/2a -2/2 = -1
f(-1) = (-1)² + 2(-1) + 1 = 1 -2 + 1 = 0

(-1.0) is the vertex

and x = -1 is the axis of symmetry
create an xy table
f(0)=0² + 2(0) + 1 = 1
f(1) = (1)² +2(1) + 1 = 4
x y
0 1
1 4
Now graph


Now Solve
Solving x² + 2x + 1 = 0
We can solve easily but let’s use the quadratic formula

= -1






The solution set is {-1}

Number of roots: 1 real root Number of x- intercepts: one

Example 3: x² -4x + 7 = 0

find –b/2a=        +4/2 = 2
f(2) = (2)² -4(2) + 7 = 4 -8 + 7 = 3

vertex ( 2, 3)
and x= 2 is the axis of symmetry

create an xy table
f(1) = (1)² -4(1) + 7
f(0) = (0)² -4(0) + 7
x y
1 4
0 7
Now graph
Now solve
x² -4x + 7 = 0

There is NO REAL number root since does not represent a real number

Number of roots: no real number roots Number of x intercepts: None


In each of these examples the value of b²-4ac in the quadratic formula is the key to the number of real roots.

When b²-4ac is negative, there is no real number root of the equation ax² + bx + c = 0 because square roots of negative numbers do not exist in the set of real numbers.

Because the value of b²-4ac discriminates, or points out differences, among these 3 cases above, it is called the discriminant of the quadratic equation.

The discriminant is only part of the quadratic formula and simpliy helps one determine the number of roots.

Math 6 Honors ( Periods 1, 2, & 3)

Negative Numbers 11-1

On a horizontal number line we use negative numbers for the coordinates of points to the left of zero. We denote the number called ‘negative four’ by the symbol -4. The symbol -4 is normally read ‘ negative 4’ but we can also say ‘ the opposite of 4.’

The graphs of 4 and -4 are the same distance from 0—>but in opposite directions. Thus they are opposites. -4 is the opposite of 4.

The opposite of 0 is 0

Absolute Value is a distance concept. Absolute value is the distance of a number from 0 on a number line. The absolute value of a number can NEVER be negative!!

Counting (also known as Natural) numbers: 1, 2, 3, 4, ….
Whole numbers 0, 1, 2, 3, 4….
Integers are natural numbers and their opposites AND zero
…-4, -3, -2, -1, 0, 1, 2, 3, 4….

The opposite of 0 is 0.

The integer 0 is neither positive nor negative.

The farther we go to the right on a number line--- the bigger the number. We can compare two integers by looking at their position on a number line.

if x < 0 what do we know? x is negative number if x > 0, what do we know? x is a positive number

We have been practicing representing integers by their graphs, that is, by points on a number line.

Make sure that your number line includes arrows at both ends and a line indicating where zero falls on your number line.
The graph of a number MUST have a closed dot right on the number line at that specific number.
Please see our textbook page 366 for an accurate example.