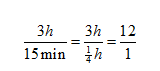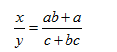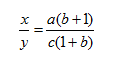Algebra Honors ( Periods 6 & 7)

Percents 7-5

You have been doing THIS since 6^th grade ( or even  before!)

The word percent means per cent or hundredths or divided by 100.

29 percent = 29%= 29/100 = 0.29

2.6 percent = 2.6% = 2.6/100 = 26/1000 = 0.026

637 percent = 637% = 637/100 = 6  37/100 = 6.37

0.02 percent = 0.02% = 0.02/100 =  2/10,000 = 0.0002

¼ percent = ¼% = 0.25% = 0.25/100 = 25/10,000 = 0.0025

33 ⅓ percent = 33 ⅓% = 100/3% = 100/3 ÷ 100 = 1/3

It is easy to translate word problem questions about percents if you use the methods reviewed in class:

Translating into AN EQUATION

Remember  when translating into an equation “is” means =  and “of” means multiplication
Change the % into a decimal ( or fraction)

Example 1

15%   of   180    is    what number?

0.15 (180)   =   x

or as a fraction

(15/100) (180) = x

In both cases you ge

x = 27

So 15% of 180 is 27.

Example 2

23 is 25% of what number?

23 = .25(x)

or as a fraction

23 = (25/100)(x)

Again in both cases you will arrive at

x = 92

23 is 25% of 92

Example 3

What percent  of 64  is 48?

x(64) = 48

This time you need to remember you found

x = 48/64 which simplifies to ¾

You need to remember to change this into a % 

 ¾ = 75%

This is more easily done using a fraction

(x/100)(64) = 48

x = 75

You just need to remember to add the percent symbol!

Let’s use those three examples but using the proportion method;

Translating into A PROPORTION

Remember  when translating into a proportion “is” means part  and “of” means whole
Change the % into a fraction  with 100 as the denominator. You will have 3 out of 4 numbers. The one missing is the one you are solving for—in each problem

  

That’s all you need to remember

Example 1

15%   of   180    is    what number?

You definitely want to simplify before using cross products

but you will get

x = 27

Example 2

23 is 25% of what number?

You definitely want to simplify before using cross products

but you will get

x = 92

Example 3

What percent  of 64  is 48?

You definitely want to simplify before using cross products

but you will get

x = 75

so it is 75%

Always remember to check what the question is asking for—so you label it appropriately.

When you solve an equation with decimal coefficients, you can multiply both sides of the equation by a power of 10 (10, 100, and so on)  to get an equivalent equation with integral coefficients.

Solve    1.2x = 36 + 0.4x

Multiply both sides by 10 when the coefficients are tenths

10(1.2x)  = 10(36 + 0.4x)

12x = 360 + 4x
8x = 360
x= 45
{45}

Solve     94 = 0.15x + 0.08(1000 - x)

Multiply BOTH SIDES by 100 when the coefficients are hundredths

100(94) = 100[0.15x + 0.08(1000 - x)]

9400 = 15x +8(1000 –x)
9400 = 15x + 8000 -8x
1400 = 7x
200 = x
{200}

Word Problem Example:
During a sale, a sporting goods store gave a 40% discount on sleeping bags. How much did Ross pay for a sleeping bag with an original price of $75?

Two different methods to find the same solution:
Method 1
Find 40% of $75? 0.40 × 75 = 30
Subtract the amount of discount from the original price
75-30 = $45
Ross paid $45 for the sleeping bag

Method 2
If the sleeping bag was discounted 40%, it then cost 100% -40% or 60% of its original price
Find 60% of 75 0.60 × 75 = 45
Ross paid $45 for the sleeping bag.

Algebra Honors ( Periods 6 & 7)

Fractional Equations 7.4

The total resistance R of an electrical circuit with two resistors R₁ and R₂, that are connected in parallel is given by the formula
1/ R₁ +1/ R₂ = 1/R
What do you notice about the difference between this equation and those with fractional coefficients?

This formula is an example of a fractional equation.
An equation with a variable in the denominator of one or more terms is called a fractional equation. To solve a fractional equation, you can multiply BOTH sides of the equation by the LCD or you could use the method of solving a proportion when the equation consists of one fraction equal to another fraction.
3/x -1/4 = 1/12
The LCD of the fractions is 12x
Multiply BOTH sides of the equation by the LCD, 12x
Notice that x ≠ 0 because in this case 3/0 is undefined
12x(3/x – ¼) = (1/12)(12x)
36 -3x = x
36 = 4x
x = 9
{9}

(2-x)/(3-x) = 4/9
There are two different ways to solve this
First by finding the LCD, which is 9(3-x) Notice that x ≠3 Why?
9(3-x)[(2-x)/(3-x) = (4/9)[9(3-x)]
18-9x =12-4x
6 = 5x
6/5 = x
{6/5}
OR solve as proportion
(2-x)/(3-x) = 4/9

(2-x)(9) = (4)(3-x)
18- 9x = 12- 4x
we are at the same spot as with the first method and we arrive at the same solution
6 = 5x
6/5 = x
{6/5}

The following gets a little more complicated to do and to display here...
Solve
(2/b² - b) – 2/(b-1) = 1
Find the LCD by first factoring the denominators first
b² - b = b(b-1) so the LCD of the two fractions in this equation is in fact
b² - b BUT use it in factored form b(b-1) Notice: b ≠ 1 why?
(2/b² - b) – 2/(b-1) = 1
[b(b-1][ (2/b² - b) – 2/(b-1) ]= 1[b(b-1)]
which separates to
[b(b-1) (2/b² - b)] – [b(b-1)2/(b-1)] = 1
[b(b-1) (2/b(b - 1)] – [b(b-1)2/(b-1)] = 1
2 -2b=b(b-1)
or
2 – 2b = b² - b
solve for b now
0 = b² - b + 2b -2
0 = b² + b – 2
0 = (b-1)(b+2)
b = 1 and b = -2
Remember in this case b ≠ 1 because of the ORIGINAL EQUATION
the solution set is only
{-2)

Multiplying both sides of an equation by a variable expression sometimes results in an equation that has an extra root. You must check each root of the transformed equation to see if it satisfies the original equation.

Math 6A (Periods 1 & 2)

Graphs of Ordered Pairs 11-8

A PAIR of numbers whose ORDER is important is called an
ordered pair!!
(ordered, pair)

(2,3) is not the same as (3,2)

The two perpendicular lines are called axes.
The x-axis deals with the 1st number of the ordered pair and the y-axis deals with the 2nd number of the ordered pair.
The AXES meet at a point called the Origin (0,0)
The plane is called the coordinate plane

There are 4 quadrants, Use Roman Numerals to name them!!
Quadrant I ---> both the x and y coordinates are positive
(x,y) (+,+)

Quadrant II --> the x coordinate is negative but the y is positive
(-x,y) (-,+)

Quadrant III -->. both the x and y coordinates are negative
(-x,-y) (-,-)

Quadrant IV --> the x coordinate is positive but the y coordinate is negative
(x,-y) (+,-)

Algebra Honors ( Periods 6 & 7)

Ratios 7-1

The ratio of one number to another is the quotient when the first number is divided by the second number (and the 2nd number does not equal 0) 

Ratios = fractions with meaning 

A ratio is the comparison of a number a and a non zero number b using division. The ratio a to b can be written three ways-- and you read them all the same

1) as a quotient using the division sign ÷   1 ÷ 3

32) as a fraction  1/3

3) as a ratio using a colon  1:3

A ratio of 7 to 4 can be written 7:4 or 7/4
A Ratio needs two numbers. DO NOT make it into a Mixed number!

32:48 becomes 2:3

   = 3x/2y

You can use ratios to compare 1 quantities of the SAME KIND

To write the ratio of two quantities of the same kind

1) First express the measures in the same unit

2) Then write their ratio

Write each ratio in simplest form

3h: 15 min

or 12:1

That’s the same ratio whether you changed the numerator to minutes or the denominator to hours

9in: 5 ft

Write a ratio of the height of a tree 4m tall to the height of a sapling 50cm tall

1) Express both heights in centimeters

2) Express both heights in meters

When you solve a word problem, you may need to express a ratio in a different form. If two numbers are in the ratio 3:5 you can use 3x and 5x to represent them, because

The lengths of the sides of a triangle are in the ratio 3:4:5. The perimeter of the triangle is 24 in. Find the lengths of each side.

Let the lengths of the sides be 3x, 4x, and 5x

3x + 4x + 5x = 24

12x= 24

x = 2

So the sides of the triangle are 6in, 8 in, and 10 in

Find the ratio of x to y 
Collect x-terms on one side and y terms on the other. Then factor

3x = 7y

Divide both sides by 3 and then divide both sides by y

cx –ay = aby - bcx

collecting  the x terms on one side and the y terms on the other you have

cx + bcx = aby + ay

Now factor

x(c + bc) = y( ab + a)

divide both sides by c + bc

then divide both sides by y

you have

BUT… you can still factor

which can simplify to