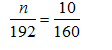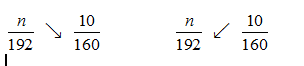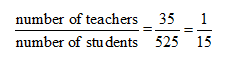Math 6A ( Periods 1 & 2)

Proportions 7-7

Let’s continue our discussion of mythical middle schools

The 6^th grade class at Madison Middle School has 160 students and 10 teachers.

The 6^th grade class at Jefferson Middle School has 144 students and 9 teachers.

Let’s compare the two teacher to student ratios!

Thus the two ratios are equal

An equation that states that two ratios are equal is called a proportion.

The proportion above may be read as

10 is to 160   AS    9 is to 144

The numbers 10, 160, 9, and 144 are called the TERMS of the proportion.

Sometimes (especially in this textbook!) one of the terms of the proportion is missing—or is a variable.

For example, 

Let’s say we know that next year the student population  at Madison will be at 192 students. How many teachers will be needed if the teacher to student ratio is to remain the same?

First, write a “let statement” to identify your variable

Let n = the number of teachers needed next year

Then, if the teacher to student ratio is to be the same, we must have

To solve this proportion, we find the value of the variable that makes this equation true.

This can be done by finding equivalent fractions with a common denominator…

 Since the denominators are equal the numerators must also be equal so we have 160n = 10(192)

What do you do NOW?

divide carefully

n = 12

Notice that this results could also have been obtained by cross-multiplying in the original proportions. That is

to get

160n = 10(192)

n = 12

There for the school will need 12 teachers next year.

Property of Proportions                        

 with b≠  0 and d ≠ 0       Then ad = bc

3n = 8(12)

3n = 96

divide both sides by 3

n =  32

But WAIT—could you have done this another way?

Sure

What do you do to 3 to get 12? ( multiply by 4)

… so what must you do to 8?  ( multiply by 4)

that’s a great check.

So what happens if you have

from the textbook we learned

m² = 3(27)

m² = 81

Now, we have worked with square roots before—so you should be able to solve this problem.

Chapter 5 covered square roots.

Technically, you perform the following

m= 9

Algebra Honors ( Period 6 & 7)

Determining an Equation of a Line 8-5

Write an equation of a line that has slope 2 and y-intercept 3

Easy! remember           y = mx + b

just substitute in what you have… y = 2x + 3

Write an equation of a line that has slope -4 and x-intercept 3.

This is a little different. 

The x-intercept is the x-coordinate of the point where a line crosses the x-axis. So here the point must be (3,0) so now you can substitute into y=mx + b and find b.

First substitute in -4 for m  y = -4x +b

To find b , substitute 3 for x and 0 for y in y = -4x + b

so

0=-4(3) + b

0=-12 + b

12=b

Therefore the equation must be y = -4x + 12

Write an equation of the line passing through the points ( -2, 5) and ( 4, 8)

Since it doesn't give us the slope, we must find it using

   

Substitute  ½ for m in y = mx + b

y =  x/2 + b

Choose one of the points, say (4, 8) and substitute 4 for x and 8 for y.

8 = (1/2)(4) + b

8 = 2 + b

6 = b

Therefore the equation is y = (1/2)x + 6

or y = x/2 + 6

Note: that we could have used the point ( -2, 5) and the resulting equation would have been the same!

Write an equation in STANDARD FORM for the following line described

The line that is parallel to x – 2y + 7 = 0 and contains ( -4, 0)

The first thing we need to do is change the given line into slope-intercept form 

y = mx + b

-2y = -x – 7  becomes   y = x/2 + 7/2

If the line we are trying to find is parallel to that line its slope must also be ½

Now using y = mx + b and the point on the line

0 = (1/2)(-4) + b

0= -2 + b

b = 2

so the line is y = x/2 + 2

BUT that is not in standard form Ax + By = C

Where A, B, and C are integers and A is a  whole number

-x/2 + y = 2

Now multiply everything by -2

x- 2y = -4

Find a line passing through ( -2, 3), (2, 5) and (6, k)  Find k

First find the slope using the two given points

y = (1/2)x +b

Using ( -2,3)

3 = (1/2)(-2) + b

3 = -1 + b

4 = b

y = (1/2)x + 4  is the equation of the line so to solve for k

k = (1/2)(6) + 4

k = 3 + 4 = 7

Math 6A (Periods 1 & 2)

Ratios 7-6

In one of our our textbook, the example given involves the number of students --at what I called a mythical middle school --as well as the number of teachers. There are 35 teachers and 525 students. We can compare the number of teachers to the number of students by writing a quotient

35

525

1/15

The quotient of one number divided by a second number is called the ratio of the first number to the second number.

We can write a ratio in the following ways:

1/15                 1:15                              1 to 15

All of these expressions are read   one to fifteen.

If the colon notation is used the first number is divided by the second. A ratio is said to be lowest terms if the two numbers are “relatively prime.”

You do not change an improper fraction to a mixed number if the improper fraction represents a ratio

There are 9 players on a baseball team. Four of these are infielders and 3 are outfielders. Find each ratio in lowest terms.

a. infielders to outfielders

b. outfields to total players

# of  infielders

# of outfielders

= 4/3  or  4:3 or 4 to 3

# of outfielders

# total of players

= 3/9 = 1/3  or  1:3   or 1 to 3

Some ratios compare measurements. In these cases we must be sure the measurements are expressed in the same units

It takes Aaron ( or Austin)  4 minutes to mix some paint for his science project. It takes him 3 hours to complete painting his science project. What is the ratio of the time it takes Aaron ( or Austin) to mix the paint to the time it takes Aaron ( or Austin) to paint his project?

Use minutes as a common unit for measuring time. You must convert the hours to minutes first

3h = 3 · 60min = 180 min

The ratio is :

min to mix

min to paint

  =   4/180 = 1/45    or 1:45

Some ratios are in the form

 40 miles per hour   or 5 pencils  for a dollar

“ I want my… I want my…. I want my … MPG!!”

These ratios involve quantities of different kinds and are called rates. Rates may be expressed as decimals or mixed numbers. Rates should be simplified to a per unit form. When a rate is expressed in a per unit form, such a rate is often called a  unit rate.

Amir’s dad’s car went 258 miles on 12 gallons of gas. Express the rate of fuel consumption in miles per gallon.

The rate of fuel consumption is

258 miles

12 gallons

= 21 1/2 miles per gallon

Some of the most common units in which rates are given are the following:

mi/gal or mpg                                                  miles per gallon

mi/h or mph                                                     miles per hour

km/L                                                                kilometers per liter

km/h                                                                kilometers per hour

This will be 2nd day:

A baseball players batting average is the ratio of the number of hits to the number of office times at bat.
Example is Nomar Garciaparr who got 190 hits in his 523 times at bat.
190/5332 = 5/14
Normally, batting averages are given as decimals rounded to the nearest thousandths. But we can write this ratio as 5:14 or as " 5 to 14."

We then compares two ratios. We looked at two different fish tanks
tank A had 2 fish in it and was 40 quarts
Tank B had 3 fish in it and was 15 gallons

Fish in Tank A   2 fish
Fish in Tank B   3 fish

2
3

Volume in Tank A
Volume in Tank B

40 quarts
15 gallons

WAIT-- we must compare quantities in terms of common units. When a common unit is used, the ratio a:b does NOT have units!
4 quarts = 1 gallon so 40 quarts must be 10 gallons

10 gallons
15 gallons

10/15 = 2/3

The two ratios are equal

Comparing Three Ratios
We compared the records of three soccer teams from three different schools
Chestnut HS   wins:  10   AND losses: 8
Mae Jennison wins:  12   AND losses: 8
Buena Vista  wins:  16   AND losses: 12

Which team had the best record?
Two Methods:
A. Find the team with the greatest ratio of wins to losses

Chestnut :  10/8 = 5/4
Mae Jennison: 12/8 = 3/2
Buena Vista:  4/3

Mae Jennison has the best record
B. Find the team with the greatest ratio of wins to TOTAL games:



Chestnut: 10/18 = 5/9
Mae Jennison: 12/20 = 3/5
Buena Vista: 16/28 = 4/7

Because 3/5= 0.6 is greater than 5/9 (5/9= 0.55555) or 4/7( 4/7= 0.5714...)
Mae Jennison has the best record

Notice we change the fractions to decimals to compare. However, you can use your skills with fractions to easily compare the fractions.Page 229
1 What is the cost of grapes in dollars per kilogram if 4.5 kg of grapes costs $7.56?
$7.56/4.5 kg divide carefully and you discover it is $1.68/kg
2. THe index of refraction of a transparent substance is the ratio of the speed of light in space to the speed of light in the substance.
Using the table from the textbook (look at page 229) Find the index of refraction of
a) glass
300,000/200,000 straight from the chart, which can simplify to 3/2
b) water
300,000/225,000 again from the chart, which can simplify to 4/3

3. The mechanical advantage of a simple machine is the ratio of the weight lifted by the machine to the forse necessary to lift it.
What is the mechanical advantage of a jack that lifts a 3200 pound car with a force of 120 pounds?
3200/120 = 80/3

4. The C string of a cello vibrates 654 times in 5 seconds. How many vibrations per second is this?
654 vibrations/5seconds... divide carefully and you find... 130 4/5 vibrations per second

5. A four-cubic-foot volume of water at sea level weights 250 pounds. What is the density of water in pound per cubic foot?
250 pounds/4 cubic ft ... divide carefully and you find 62 1/2 lb/ft³

6. A share of stock that costs $88 earned $16 last year. What was the price to earnings ratio?
88/16 = 11/2

7. we did in our spiral notebooks this year... please check