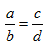Math 7 ( Period 4)

Solving  Percent Problems 7.5

There are 2 methods: Equations and Proportions

For both methods, there are THREE parts of any percent problem:

1) the BASE à the number you are taking a percent of

2) the PERCENT rateà the percent

3) the PERCENTAGE AMOUNT à (base)(%)

EQUATION METHOD:

Just translate and solve for the missing number.

Remember:

isà =

of à multiply

EXAMPLES:

Finding the PERCENTAGE AMOUNT

Find 60% of 15

First realize that “Find” means “What is”

and change the percent to a decimal or a fraction

so

What is 60% of 15

n = (.60)(15)

n = 9

Using fractions we found

first that 60/100 simplifies to 3/5

so

n =(3/5)(15)

That simplifies to

n = 9

Finding the BASE:

35% of what number  is 52.5

.35n = 52.5

simple one step equation

.35n/.35 = 52.5/.35

n = 150

Again, what if we used fractions

35% = 35/100 = 7/20

so

(7/20)n = 53.5

n = 150

Finding the PERCENT rate

What percent of 25 is 13?

25p = 13

p = 13/25

Now you need to make this a percent and that can be accomplished by dividing

but you can also use equivalent fractions   that is,

13/25 = 52/100 so that is 52%

PROPORTION METHOD

%/100 = is/of

Set this up each time and then substitute in what you know

Firstà look for the 5 rate and put that in ( if you are given it)

Second à find  either the “of” or the “is”

Lastà  Whatever is missing is what you are finding…

We did the three examples above as proportions

EXAMPLES:

Find 60% of 15

60/100 = x/15

Simplify and you get

3/5 = x/15

you can simplify even more and get

3/1 =x/3

so x = 3(3) = 9

35% of what number  is 52.5

35/100 = 52.5/x

Simplifying again we get

7/20 = 52.5/x

Using cross products

7x = 20(52.5)

7x = 1050

so x = 150

What percent of 25 is 13?

This is the only one where we do not have the %

n%/100 = 13/25

Can we simplify first?

Yes

n%/4 = 13/1

so n = 4(13)

n = 52

Remember to add the percent sign

52%

Math 7 ( Period 4)

Scale Drawings & Models  7.3

A scale drawing is a diagram of an object in which the length and the width are proportional to the actual length and width of the object

The scale for the drawing gives the relationship between the drawing’s measurement and the actual measurements, such as “ 1 in : 2ft.” 

This scale means that 1 inch on the drawing represents the actual distance of 2 feet.

The scale factor for a scale drawing is the ratio of the length and width in the drawing to the corresponding actual length and width (in the same units of measurements)  for instance a sale of “.25 in : 2 ft” has a scale factor of  1/96 because you need to change either the inches to feet in the numerator  or the feet to inches in the denominator to have the same units of measurement. 

2 ft is equivalent to 24 inches so you have  .25/24 when you simplify that you get 1/96

Scale ratios are usually rates… They have two different labels.
1.5 in : 1000 miles.

Scale rates have NO LABELS at all because both the model and the actual are expressed in the same label.  The scale rate no longer has any labels and simplifies.

Using cross products you find that the missing  side is 12 inches

ALWAYS SET UP THE PROPORTION WITH 2 KNOWN MEASUREMENTS.

We looked at the scale drawing of the theater stage on Page 328 and found the length of the back wall. 
In the scale drawing .25 inches  = 2 ft  . 

The back wall in the drawing measures 1.5 inches  Let x = the actual length of the back wall

We set up a proportion

 

You could simplify BEFORE you cross multiply
but without you get  .25x = 2(1.5)

divide both sides by .25

x = 12
12 feet

What if you had changed the scale to a scale  with the same units of measures first? That is changed the “.25 inches = 2 feet” to “.25 inches = 24 inches”   So

Notice the difference – now everything is in inches and when you solve it you get    x = 144

BUT THAT IS IN INCHES… 

and 144 inches = 12 feet… the same answer you arrived at—without having to change to the same units of measure!!

In Geometry the definition of similar polygons is that they have proportional sides and congruent (equal) angles. The congruent angels keep the shape the same. The proportional sides make the polygons smaller or larger. 

So if you know that 2 triangles are similar, you can find a missing measurement of a side by setting up a proportion.

Example: You know that 2 triangles are similar. One is larger than the other You know the measurement of 2 sides of the smaller  are 3 inches and 4 inches. You know that the larger triangles corresponding shorter side is 9 inches.

COMPARE PERIMETER AND AREA

Perimeter of a rectangle is 2l + 2w

So if a photo is 8 inches by 10 inches, the perimeter is
2(8) + 2(10) = 36 inches

If you reduce the size of the picture 50% on the copier
P = 2(4) + 2(5) = 18. So the perimeter is 50% smaller

Area of a rectangle = lw = 8(10) = 80 inches squared
Is the reduced photo’s area 40 inches squared?

NO 4(5) = 20 inches squares.  WHY?

each of the sides is ½ the original so (1/2)(1/2) = ¼ of the original area..

 20 is 1/4 of the original area of 80

Math 7 (Period 4)

Writing & Solving Proportions 7.2

An equation that states tow ratios are equal is called a proportion.

The proportion  

 is read “ a is to b as c is to d.”

It has two cross
products ad and bc.

In words: In a proportion the cross products are equal

In Algebra: if 

 then ad = bc

With examples: because 2/5 = 4/10 you know that 2(10) = 4(5)

When you know three numbers in a proportion, you can find the missing value by using cross products

Use cross products property to solve the proportion  

3(15) = 5(m)
Now it is a one step equation
Divide both sides by 5

3(15)/5 = 5m/5
9 = m

Be sure to compare quantities in the same order in a proportion.

You are reading a novel—we talked about The Giver, one day you read 30 pages in 50 minutes. The next day you read 24  more pages in 40 minutes. Did you read at the same rate?

Setup a proportion

Does     

Notices on both the pages are in the numerator and the minutes are in the denominator.

Could we have written it  

 Yes.  Notices on both the pages are in the denominator now and the minutes are in the numerator.

We looked at the CORN BREAD RECIPE on Page 336

Amount	Ingredient	Directions
1  ¼ c	flour	Pre heat oven to 400 º
¾  c	Corn meal	Grease 8 by 8 inch pan
¼ c	sugar
2 t	Baking powder	Combine dry ingredients. Mix in milk,
1 c	Skim milk	oil and egg. Pour into pan. Bake 20
½ t	salt	to 25 minutes
¼ c	oil
1	Egg, beaten	9 servings

If you had 8 cups of corn meal, how many loaves of corn bread could you make?  Set up a proportion

  (3/4)x = 8  solve 

 x = 32/3 which is  10 2/3 so you could make 10 loaves

To make 10 loaves of corn bread, how much sugar would you need?

Again set up a proportion

  Solve 10(¼) = s   10/4 = s or 2½ cups of sugar

Math 6A ( Periods 1 & 2)

Solving Equations 11-7

Now that we have learned about negative integers, we can solve an equation such as
x + 7 = 2
We need to subtract 7 from both sides of the equation
x + 7 = 2
- 7 = - 7

to do this use a side bar and use the rules for adding integers
Notice the signs are different so
ask yourself... Who wins? and By How Much?
stack the winner on top and take the difference
so
x + 7 = 2
- 7 = - 7
x = -5



t - -10 = 19
becomes -- with add the opposite---
t+ + 10 = 19
which is just
t + 10 = 19
so subtract 10 from both sides
t + 10 = 19
- 10 = - 10
t = 9

w - - 26 = -44
"Add the Opposite"
w + + 26 = -44
- 26 = - 26
x = -70

Know your integer rules and it becomes easy!!
Side bars are great, if you need them with difference signs!!


y -^- 6 = 4
add the opposite and you get
y + 6 = 4
now you need to subtract 6 from both sides of the equation
y + 6 = 4
- 6 = - 6
Again the signs are different -- ask your self those all important questions
"Who Wins? and "By How Much?"
Use a side bar, stack the winner on top and take the difference. Make sure to use the winner's sign in your answer!!
y = 2

What about -5u = 125?
Whats happening to u?
It is being multiplied by -5... so you must divide by -5

-5u = 125
-5 -5
u = -25

or written easier to read -5u/-5 = 125/-5
u = -25

(1/-9)c = 33
Need to multiply both sides by the reciprocal of (1/-9) which is (-9/1)

(-9/1)(1/-9)c = 33(-9/1)
c = -297



2- STEP EQUATIONS

What about

3u - 1 = -7
You need to do the reverse of PEMDAS... remember unwrapping the present? We did the exact opposite of what we had done to wrap the present!!
so
3u - 1 = -7
+ 1 = + 1
3u = -6
Now divide by 3 on both sides
3u/3 = -6/3
u = -2


3z - ^- 15 = 9
add the opposite first and you get
3x + 15 = 9
In order to solve this 2 step equation
we need to do the reverse of PEMDAS-- as we did with unwrapping the present so many months ago
3x + 15 = 9
subtract 15 from both sides of the equation
3x + 15 = -9
- 15 = - 15

This time the sides are the same-- so just add them and use their sign
3x + 15 = -9
- 15 = - 15
3x = -24
Now divide both sides by 3
3x = -24
3 3

x = -8

Make sure to BOX your answer!!
What about this one
(1/2)(x) + 3 = 0
subtract 3 from both sides
(1/2)x = -3

Multiple by the reciprocal of 1/2 which is 2/1
(2/1)(1/2)x = -3(2/1)
x = -6
Again box your answer.



What about x = -6 + 3x
OH dear... we have variables on BOTH sides of the equations... we need to get the variables on one side all the constants on the other.
We need to isolate the variable!!

x = -6 + 3x
What if we add six to both sides
x = -6 + 3x
+6 = + 6
x + 6 = 3x
now we need to subtract x from both sides
x + 6 = 3x
- x - x
6 = 2x
so now divide both sides by 2
6/2 = 2x/2
3 = x

How about this one
3 - r = -5 + r
- 3 = - 3
-r = -8 + r
if subtract r from both sides, I will get rid of the +r on the right side

-r = -8 + r
- r = -r
-2r = -8
Now divide by -2 on both sides

-2r/-2 = -8/-2
r = 4

Math 6A ( Periods 1 & 2)

Quotients of Integers 11-6
Now that we have learned about negative integers, we can solve an equation such as
x + 7 = 2
We need to subtract 7 from both sides of the equation
x + 7 = 2
- 7 = - 7

to do this use a side bar and use the rules for adding integers
Notice the signs are different so
ask yourself... Who wins? and By How Much?
stack the winner on top and take the difference
so
x + 7 = 2
- 7 = - 7
x = -5



t - -10 = 19
becomes -- with add the opposite---
t+ + 10 = 19
which is just
t + 10 = 19
so subtract 10 from both sides
t + 10 = 19
- 10 = - 10
t = 9

w - - 26 = -44
"Add the Opposite"
w + + 26 = -44
- 26 = - 26
x = -70

Know your integer rules and it becomes easy!!
Side bars are great, if you need them with difference signs!!


y -^- 6 = 4
add the opposite and you get
y + 6 = 4
now you need to subtract 6 from both sides of the equation
y + 6 = 4
- 6 = - 6
Again the signs are different -- ask your self those all important questions
"Who Wins? and "By How Much?"
Use a side bar, stack the winner on top and take the difference. Make sure to use the winner's sign in your answer!!
y = 2

What about -5u = 125?
Whats happening to u?
It is being multiplied by -5... so you must divide by -5

-5u = 125
-5 -5
u = -25

or written easier to read -5u/-5 = 125/-5
u = -25

(1/-9)c = 33
Need to multiply both sides by the reciprocal of (1/-9) which is (-9/1)

(-9/1)(1/-9)c = 33(-9/1)
c = -297



2- STEP EQUATIONS

What about

3u - 1 = -7
You need to do the reverse of PEMDAS... remember unwrapping the present? We did the exact opposite of what we had done to wrap the present!!
so
3u - 1 = -7
+ 1 = + 1
3u = -6
Now divide by 3 on both sides
3u/3 = -6/3
u = -2


3z - ^- 15 = 9
add the opposite first and you get
3x + 15 = 9
In order to solve this 2 step equation
we need to do the reverse of PEMDAS-- as we did with unwrapping the present so many months ago
3x + 15 = 9
subtract 15 from both sides of the equation
3x + 15 = -9
- 15 = - 15

This time the sides are the same-- so just add them and use their sign
3x + 15 = -9
- 15 = - 15
3x = -24
Now divide both sides by 3
3x = -24
3 3

x = -8

Make sure to BOX your answer!!
What about this one
(1/2)(x) + 3 = 0
subtract 3 from both sides
(1/2)x = -3

Multiple by the reciprocal of 1/2 which is 2/1
(2/1)(1/2)x = -3(2/1)
x = -6
Again box your answer.



What about x = -6 + 3x
OH dear... we have variables on BOTH sides of the equations... we need to get the variables on one side all the constants on the other.
We need to isolate the variable!!

x = -6 + 3x
What if we add six to both sides
x = -6 + 3x
+6 = + 6
x + 6 = 3x
now we need to subtract x from both sides
x + 6 = 3x
- x - x
6 = 2x
so now divide both sides by 2
6/2 = 2x/2
3 = x

How about this one
3 - r = -5 + r
- 3 = - 3
-r = -8 + r
if subtract r from both sides, I will get rid of the +r on the right side

-r = -8 + r
- r = -r
-2r = -8
Now divide by -2 on both sides

-2r/-2 = -8/-2
r = 4

Math 7 (Period 4)

Ratios & Rates 7.1

Ratios = fractions with meaning (it is ALL about the labels!)
A ratio is a comparison of a number a and a nonzero number b using division. The ratio a to b can be written in three ways—and you read them all the same!

You can write it as a  (1) fraction    a/b  (2)    a:b  or (3) “a to b”
and all three (including your fraction) are read “a to b” 

Anything you can do with a fraction – you can do with a ratio… but a ratio needs two numbers!

Rates = ratios with 2 different labels
miles per gallon and miles per hour are the two most known rates.

A rate of “a per b” is a type of ratio that compares two different quantities, a and b that have different units of measure.

Unit Rates = rates with a denominator of 1 (it still needs to have different labels)
I drive 150 miles in 3 hours  that’s a rate  changing it to a unit rate, simply divide the numerator by the denominator
150 miles/3 hours = 50 mph    now that that’s a unit rate

People focus on MPG these days when they buy cars.
A Honda civic =40mpg while a Hummer = 8mpg

A special unit rate is called the unit price

We talked about how people decide whether to go to CostCo or Pavilions to purchase items, such as “goldfish”

$7.99 at Pavilions for 33.5oz and
$10.99 at CostCo for 48oz

If you divide $/oz you get a unit rate known as the UNIT PRICE

MONEY must be in the numerator

Algebra Honors ( Periods 6 & 7)

Solving Problems Involving Quadratic Equations 12-6

You can use quadratic equations to solve problems...
We used the examples in the book to start with:

The park commission wants a new rectangular sign with an area of 25 m² for the visitor center. The length of the sign is to be 4 m longer than the width . To the nearest tenth of a meter, what will be the length and the width of the sign?
Always make sure you check before AND after-- to see what the problem is really asking for...
Let x = the width in meters
then x + 4 = the length in meters

Use the formula for the area of a rectangle to write an equation

x(x+4) = 25
solve it
x(x +4) = 25 becomes
x² + 4x = 25
You can use two methods: the quadratic formula would be my second choice since completing the square works easily here

x² + 4x + 4 = 25 + 4
(x + 2)² = 29
x + 2 = ±√29
You can use your calculator, or the table of square roots... or approximately easily using the method taught in class earlier this year
but to the nearest tenth you get
-2 + √29 ≈3.4
-2 - √29 ≈-7.4

Since you can't have a negative root since a negative length has no meaning... you know the width must be about 3.4 meters and therefore the length is 3.4 +4 or approximately 7.4 meters

Problem 2:
The sum of a number and its square is 156. Find the number

Let x = the number
then
x² + x = 156

x² + x - 156 =0
Using the skills you have for factoring
(x +13)(x-12) = 0
so
x = 13 and x = 12
You have two solutions to this question!!

Problem 3:
The altitude of a triangle is 9 cm less than the base. The area is 143 cm²
What are the altitude and base?

Remember the formula for the area of a triangle is A = ½bh

Let b = the length of the base
then the altitude ( the height) is b-9
so
½(b)(b-9) = 143
b² -9b = 286
b² -9b - 286 = 0
(b -22)(b +13) = 0
b = 22 and b= -13
You can't have a negative length so
the base is 22 cm and the altitude is 13 cm


An object that moves through the air and is solely under the influence of gravity is called a projectile. The approximate height (h) in meters of a projectile at t seconds after it begins its flight from the ground with initial upward velocity v₀ is given by the formula
h = -5t² + v₀t
We can find when such a projectile is at ground level (h=0) by solving
0 = -5t² + v₀t.
If a projectile begins its flight at height c, its approximate height at time t is
h = -5t² + v₀t + c .
We can find when it hits the ground by solving h=0 or
0 = -5t² + v₀t +c.

When a projectile is thrown into the air with an initial vertical velocity of r feet per second, its distance (d) in feet above the starting point t seconds after it is thrown is approximately
d = rt – 16t²