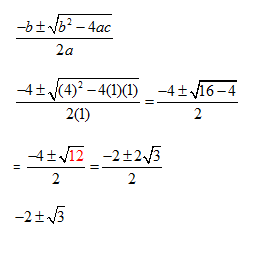Graphs of Quadratic Equations: The Discriminant 12-4
Sometimes it is NOT necessary to draw the graph of an equation.
Knowing the relationships between an equation and its graph— you can obtain important information from the equation itself.
Today’s lesson illustrates the relationship between the number of roots of a quadratic equation and the number of x-intercepts of the related parabola.
In the parabola the x coordinate of a point where the curve intersects the x axis is called an x-intercept of the curve.
Looking at the parabola on page 572 you notice that this parabola has two x-intercepts, -1 and 3 because y = 0 for both of these values of x.
you can also see that
x2- 2x – 3 = 0 or (x +1)(x-3) = 0
has -1 and 3 as its roots, solutions, zeros… {-1,3}
The algebraic fact that a quadratic equation can have two, one or no real number roots corresponds to the fact that a parabola can have two, one or no x-intercepts…
and we can find that out by just working with the quadratic equations—rather than having to graph…
However… let’s graph a few
Example 1: x2 + 4x + 1 = 0
find –b/2a
-4/2 = -2
f(-2) = (-2)2 + 4(-2) + 1 = 4 -8 + 1 = -3
so (-2,-3) is the vertex
x = -2 is the axis of symmetry
Create an x y table
f(-1) = (-1)2 +4(-1) + 1 = 1 -4 +1 = -2
f(0) = 02 + 4(0) + 1 = 1
x y
-1 -2
0 1
Now solve
Solving x2 + 4x + 1 = 0
Now graph
Number of roots: two real roots Number of x-intercepts: two
Example 2 : x2 + 2x + 1 = 0
find -b/2a -2/2 = -1
f(-1) = (-1)2 + 2(-1) + 1 = 1 -2 + 1 = 0
(-1.0) is the vertex
and x = -1 is the axis of symmetry
create an xy table
f(0)=02 + 2(0) + 1 = 1
f(1) = (1)2 +2(1) + 1 = 4
x y
0 1
1 4
Now graph
Now Solve
Solving x2 + 2x + 1 = 0
We can solve easily but let’s use the quadratic formula
= -1
The solution set is {-1}
Number of roots: 1 real root Number of x- intercepts: one
Example 3: x2 -4x + 7 = 0
find –b/2a= +4/2 = 2
f(2) = (2)2 -4(2) + 7 = 4 -8 + 7 = 3
vertex ( 2, 3)
and x= 2 is the axis of symmetry
create an xy table
f(1) = (1)2 -4(1) + 7
f(0) = (0)2 -4(0) + 7
x y
1 4
0 7
Now graph
Now solve
x2 -4x + 7 = 0
There is NO REAL number root since does not represent a real number
Number of roots: no real number roots Number of x intercepts: None
In each of these examples the value of b2-4ac in the quadratic formula is the key to the number of real roots.
When b2-4ac is negative, there is no real number root of the equation ax2 + bx + c = 0 because square roots of negative numbers do not exist in the set of real numbers.
Because the value of b2-4ac discriminates, or points out differences, among these 3 cases above, it is called the discriminant of the quadratic equation.
The discriminant is only part of the quadratic formula and simpliy helps one determine the number of roots.
If b2-4ac < 0 "no real number roots"
If b2-4ac = 0 "one rational root"
If b2-4ac > 0 " two real number roots" we can break this down even more specific:
If b2-4ac is a perfect square then " two rational roots"
If b2-4ac is a non-square then "two irrational roots"
Friday, March 28, 2014
Thursday, March 27, 2014
Algebra Honors ( Periods 6 & 7)
Methods of Solutions 12-5
You have learned five different methods of solving quadratics.. picking the best one is the challenge
Here are some tips on when to use each method:
Quadratic Formula--> when to use: ax2 +bx + c = 0 (It always works) Great when you have a calculator
Factoring--> when to use: ax2 +bx + c = 0 you see the factors easily or you have ax2 +bx = 0
Using the Property of SQRT's --> when to use: ax2 + c = 0
Completing the square --> when to use: x2 +bx + c = 0 especially when b is even
Graphing... this really does takes time but if done correctly... it really shows what are the roots... and.... the x-intercepts, the solutions, the zeroes...
Which method would you use for the following?
x2 +5x - 6 = 0
Answer: Factoring
x2 -2x = 1
Answer: Completing the square
11x2 = 44
Answer: SQRTing
3x2 -5x = 4
Answer: Quadratic Formula

You have learned five different methods of solving quadratics.. picking the best one is the challenge
Here are some tips on when to use each method:
Quadratic Formula--> when to use: ax2 +bx + c = 0 (It always works) Great when you have a calculator
Factoring--> when to use: ax2 +bx + c = 0 you see the factors easily or you have ax2 +bx = 0
Using the Property of SQRT's --> when to use: ax2 + c = 0
Completing the square --> when to use: x2 +bx + c = 0 especially when b is even
Graphing... this really does takes time but if done correctly... it really shows what are the roots... and.... the x-intercepts, the solutions, the zeroes...
Which method would you use for the following?
x2 +5x - 6 = 0
Answer: Factoring
x2 -2x = 1
Answer: Completing the square
11x2 = 44
Answer: SQRTing
3x2 -5x = 4
Answer: Quadratic Formula
Math 6A (Periods 1 & 2)
Products of Integers 11-4
3 ⋅ -2 = -6
Its really repeated addition
or
-2 + -2 + -2 which we learned a few sections ago was equal to -6.
The product of a positive integer and a negative integer is a negative integer.
The product of ZERO and any integer is ALWAYS ZERO!!
a⋅0 = 0
Math imitates life...and Karma(?)
What was the story I told in class... it applies to
Multiplication & Division ...
+ ⋅ + = +
- ⋅ + = -
+ ⋅ - = -
- ⋅ - = +
The product of -1 and any integer equals the opposite of that integer.
(-1)(a) = -a
The product of two negative integers is a positive integer
For a product with NO ZERO factors:
-->if the number of NEGATIVE factors is odd, the product is negative
-->if the number of NEGATIVE factors is even, then the product is positive
Every integer and its opposite have equal squares!!
Remember-- if its all multiplication use the Associative & Commutative Properties of Multiplication to make your work EASIER!!
3 ⋅ -2 = -6
Its really repeated addition
or
-2 + -2 + -2 which we learned a few sections ago was equal to -6.
The product of a positive integer and a negative integer is a negative integer.
The product of ZERO and any integer is ALWAYS ZERO!!
a⋅0 = 0
Math imitates life...and Karma(?)
What was the story I told in class... it applies to
Multiplication & Division ...
+ ⋅ + = +
- ⋅ + = -
+ ⋅ - = -
- ⋅ - = +
The product of -1 and any integer equals the opposite of that integer.
(-1)(a) = -a
The product of two negative integers is a positive integer
For a product with NO ZERO factors:
-->if the number of NEGATIVE factors is odd, the product is negative
-->if the number of NEGATIVE factors is even, then the product is positive
Every integer and its opposite have equal squares!!
Remember-- if its all multiplication use the Associative & Commutative Properties of Multiplication to make your work EASIER!!
Wednesday, March 26, 2014
Algebra Honors (Periods 6 & 7)
Imaginary Numbers
x2= -16
No real number
solutions
Imaginary number i us defined to be √-1
√-1 23
∑ ∏
I ate some pie!
All imaginary
numbers involve i
3i -5i/2 and 2i√3
i
=√-1
i2 = -1
so
x2= -16
solved over the set of imaginary numbers
x= √-16 = √16∙√-1 = 4√-1 =4i
If r > 0 then
√-r = i√r
I = √-1
i2 = -1
i3 = i∙i2 =i(-1) = -i
i4 = i2∙i2 = (-1)(-1) = 1
Monday, March 24, 2014
Algebra Honors ( Periods 6 & 7)
Quadratic Formula Song to Adele's "Rolling in the Deep"
and a second version is also on You tube... check that on out
and a second version is also on You tube... check that on out
Algebra Honors ( Periods 6 & 7)
The Quadratic Formula: 12-3
Method 5:
THE QUADRATIC FORMULA
Let's all sing it to "Pop Goes the Weasel!
" x = -b plus or minus the square root of b squared minus 4ac all over 2a
x =
-b ± √ (b2 - 4ac)
2a
Notice how the first part is the x value of the vertex -b/2a
The plus or minus square root of b squared minus 4ac represents how far away the two x intercepts (or roots) are from the vertex!!!!
Very few real world quadratics can be solved by factoring or square rooting each side.
And completing the square always works, but it long and cumbersome!
All quadratics can be solved by using the QUADRATIC FORMULA.
You will find out that some quadratics have NO REAL solutions, which means that there are no x intercepts - the parabola does not cross the x axis!
Think about what kinds of parabolas would do this....ones that are smiles that have a vertex above the x or ones that are frowns that have a vertex below the x axis.
You will find out in Algebra II that these parabolas have IMAGINARY roots
So now you know 5 ways that you know to find the roots:
1. graph
2. factor if possible
3. square root each side
4. complete the square - that's what the quadratic formula is based on!
5. plug and chug in the Quadratic Formula - This method always works if there's a REAL solution!
DON'T FORGET TO PUT THE QUADRATIC IN STANDARD FORM BEFORE PLUGGING THE VALUES INTO THE QUADRATIC FORMULA!
You should know that for the quadratic formula, you don't need the "a" coefficient to be positive!
That's important if you use factoring, SQRTing each side, and completing the square.
But for the quadratic formula, either way, you'll get the same roots!
EXAMPLE: x2 + 8x = 48
You can move the 48 over or move the x2 + 8x over and you'll get the same answers!
Let's look at:
"a" coefficient positive *****vs***** "a" coefficient negative
x2 + 8x - 48 = 0 ****VS**** -x2 - 8x + 48 = 0
First x2 + 8x - 48 = 0
-8 ± √[64 - 4(1)(-48)]
2(1)
-8 ± √(64 + 192)
2
-8 ± √(256)
2
-8 ± 16
2
(-8 + 16)/2 and (-8 - 16)/2
8/2 and -24/2
4 and -12
Now let's compare -x2 - 8x + 48 = 0
8 ± √[64 - 4(-1)(48)]
-2(1)
8 ± √(64 + 192)
-2
8 ± √(256)
-2
8 ± 16
-2
(8 + 16)/-2 and (8 - 16)/-2
24/-2 and -8/-2
-12 and 4
So all the signs are simply the opposite of each other and therefore the answers are the same
Method 5:
THE QUADRATIC FORMULA
Let's all sing it to "Pop Goes the Weasel!
" x = -b plus or minus the square root of b squared minus 4ac all over 2a
x =
-b ± √ (b2 - 4ac)
2a
Notice how the first part is the x value of the vertex -b/2a
The plus or minus square root of b squared minus 4ac represents how far away the two x intercepts (or roots) are from the vertex!!!!
Very few real world quadratics can be solved by factoring or square rooting each side.
And completing the square always works, but it long and cumbersome!
All quadratics can be solved by using the QUADRATIC FORMULA.
You will find out that some quadratics have NO REAL solutions, which means that there are no x intercepts - the parabola does not cross the x axis!
Think about what kinds of parabolas would do this....ones that are smiles that have a vertex above the x or ones that are frowns that have a vertex below the x axis.
You will find out in Algebra II that these parabolas have IMAGINARY roots
So now you know 5 ways that you know to find the roots:
1. graph
2. factor if possible
3. square root each side
4. complete the square - that's what the quadratic formula is based on!
5. plug and chug in the Quadratic Formula - This method always works if there's a REAL solution!
DON'T FORGET TO PUT THE QUADRATIC IN STANDARD FORM BEFORE PLUGGING THE VALUES INTO THE QUADRATIC FORMULA!
You should know that for the quadratic formula, you don't need the "a" coefficient to be positive!
That's important if you use factoring, SQRTing each side, and completing the square.
But for the quadratic formula, either way, you'll get the same roots!
EXAMPLE: x2 + 8x = 48
You can move the 48 over or move the x2 + 8x over and you'll get the same answers!
Let's look at:
"a" coefficient positive *****vs***** "a" coefficient negative
x2 + 8x - 48 = 0 ****VS**** -x2 - 8x + 48 = 0
First x2 + 8x - 48 = 0
-8 ± √[64 - 4(1)(-48)]
2(1)
-8 ± √(64 + 192)
2
-8 ± √(256)
2
-8 ± 16
2
(-8 + 16)/2 and (-8 - 16)/2
8/2 and -24/2
4 and -12
Now let's compare -x2 - 8x + 48 = 0
8 ± √[64 - 4(-1)(48)]
-2(1)
8 ± √(64 + 192)
-2
8 ± √(256)
-2
8 ± 16
-2
(8 + 16)/-2 and (8 - 16)/-2
24/-2 and -8/-2
-12 and 4
So all the signs are simply the opposite of each other and therefore the answers are the same
Math 7 ( Period 4)
Scientific Notation 6.9
You have had this since 5th or sixth grade... but check out the links at the bottom of these notes
Powers of ten provide a convenient way to write very large numbers. You restate very big numbers or very small numbers using powers of ten in exponential form. Numbers that are expressed as products of two factors
(1) a number greater than or equal to 1, but less than 10,
AND
(2) a power of ten
are said to be written in scientific notation.
We can write 'a number greater than or equal to 1, but less than 10' as an mathematical inequality 1 ≤ n < 10 To write a number in scientific notation we move the decimal point to the left until the resulting number is between 1 and 10. We then multiply this number by the power of 10, whose exponent is equal to the number of places we moved the decimal point. 4,592,000,000 in scientific notation First move the decimal point to the left to get a number between 1 and 10 4,592,000,000 the first factor in scientific notation becomes 4.592 Since the decimal point was moved 9 places, we multiply 4.592 by 109 to express the number in scientific notation
4.592 x 109 (Yes, you get to use the × symbol for multiplication .. but only for this!!
5,900,000,000 was given as the population of the world in 1998. I wonder what it is now? Anyone find out?
Anyway to write that large number in scientific notation it would be the product of two factors 5.9 and a power of ten
5.9 X 109
It is a way to write very large numbers AND very small numbers
Numbers expressed as products of a number greater than or equal to 1 BUT less than 10, AND a power of ten are called Scientific Notation.
Two Factors
91) 1≤ n < 10 (2) Power of 10 4,592,000,000 becomes 4.592 X 109
moved the decimal 9 places so we must multiply our number by a power of 109
98,000,000 = 9.8 X 107
320,000 = 3.2 X 105
What if I give you 7.04 X 108 and ask you to put it back into STANDARD NOTATION:
704,000,000.
0.0000207
0.0031 = 3.1 X 10-3
It isn't a negative number its just a very tiny number
1≤ n < 10 0.16 becomes 1.6 x 10 -1
0.0000207 becomes 2.07 X 10 -5
0.000345 becomes 3.45 X 10 -4
We also changed scientific notation back into standard notation ( the regular number)
9.32 X 10 -2 becomes 0.0932
we practiced some more
14,500 first we changed the number into something that fit the first factor 1 ≤ n < 10
so that becomes 1.45
Then we need to figure out how many places we moved the decimal
1.45 X 104
that works!
73,000,000 = 7.3 X 107
63,500 = 6.35 X 104
Write 3.45 X 104 into standard notation
34, 500
What happens if you are given 1/8000 this is a fraction and we need to change it to a decimal BEFORE we can write it in scientific notation
1/8000 = 0.000125
so it is
1.25 X 10-4
suppose you are multiplying two scientific notation numbers-- you do NOT need to change them into standard notation
(2.5 X 103 )(4.4 X10-5).
We found that it was
11 X 10-2
But 11 isn't 1 ≤ n < 10 so we need to change 11 into scientific notation
that alone is 1.1 X 101
Now we have 1.1 X 101 X 10-2
so 1.1 X 10-1 interesting
(6.2 X102 )( 8 X103) = (6.2)(8) X 102 X103 and
49.6 X 105 but 49.6 isn't in scientific notation
so
49.6 becomes 4.96 X101
4.96 X 101 X105 is
4.96 X 106
So
Try
(9.1 X 10-1 ) ( 5.4 X107)
(9.1)(5.4) X 10-1 X 107
So
49.14 X 106 and again 49.14 isn't in scientific notation
changing just 49.14 into scientific notation we get 4.914 X 101
so we have
4.914 X101 X 106
which
is
4.914 X 107
List from least to greatest
3.4 X 10-4 3.4 X 10-5 and 3.4 X 10-6
We noticed that the -6 exponent would be a smaller number-- when we wrote it in standard form so
3.4 X 10-6 < 3.4 X 10-5 < 3.4 X 10-4 would be the listing
Check out the following links:
this one takes you from huge numbers to teeny tiny ones
this one lets you practice scientific notation
this one lets you practice multiplying scientific notation
this one lets you practice dividing sn
this one lets you practice even harder ones!
You have had this since 5th or sixth grade... but check out the links at the bottom of these notes
Powers of ten provide a convenient way to write very large numbers. You restate very big numbers or very small numbers using powers of ten in exponential form. Numbers that are expressed as products of two factors
(1) a number greater than or equal to 1, but less than 10,
AND
(2) a power of ten
are said to be written in scientific notation.
We can write 'a number greater than or equal to 1, but less than 10' as an mathematical inequality 1 ≤ n < 10 To write a number in scientific notation we move the decimal point to the left until the resulting number is between 1 and 10. We then multiply this number by the power of 10, whose exponent is equal to the number of places we moved the decimal point. 4,592,000,000 in scientific notation First move the decimal point to the left to get a number between 1 and 10 4,592,000,000 the first factor in scientific notation becomes 4.592 Since the decimal point was moved 9 places, we multiply 4.592 by 109 to express the number in scientific notation
4.592 x 109 (Yes, you get to use the × symbol for multiplication .. but only for this!!
5,900,000,000 was given as the population of the world in 1998. I wonder what it is now? Anyone find out?
Anyway to write that large number in scientific notation it would be the product of two factors 5.9 and a power of ten
5.9 X 109
It is a way to write very large numbers AND very small numbers
Numbers expressed as products of a number greater than or equal to 1 BUT less than 10, AND a power of ten are called Scientific Notation.
Two Factors
91) 1≤ n < 10 (2) Power of 10 4,592,000,000 becomes 4.592 X 109
moved the decimal 9 places so we must multiply our number by a power of 109
98,000,000 = 9.8 X 107
320,000 = 3.2 X 105
What if I give you 7.04 X 108 and ask you to put it back into STANDARD NOTATION:
704,000,000.
0.0000207
0.0031 = 3.1 X 10-3
It isn't a negative number its just a very tiny number
1≤ n < 10 0.16 becomes 1.6 x 10 -1
0.0000207 becomes 2.07 X 10 -5
0.000345 becomes 3.45 X 10 -4
We also changed scientific notation back into standard notation ( the regular number)
9.32 X 10 -2 becomes 0.0932
we practiced some more
14,500 first we changed the number into something that fit the first factor 1 ≤ n < 10
so that becomes 1.45
Then we need to figure out how many places we moved the decimal
1.45 X 104
that works!
73,000,000 = 7.3 X 107
63,500 = 6.35 X 104
Write 3.45 X 104 into standard notation
34, 500
What happens if you are given 1/8000 this is a fraction and we need to change it to a decimal BEFORE we can write it in scientific notation
1/8000 = 0.000125
so it is
1.25 X 10-4
suppose you are multiplying two scientific notation numbers-- you do NOT need to change them into standard notation
(2.5 X 103 )(4.4 X10-5).
We found that it was
11 X 10-2
But 11 isn't 1 ≤ n < 10 so we need to change 11 into scientific notation
that alone is 1.1 X 101
Now we have 1.1 X 101 X 10-2
so 1.1 X 10-1 interesting
(6.2 X102 )( 8 X103) = (6.2)(8) X 102 X103 and
49.6 X 105 but 49.6 isn't in scientific notation
so
49.6 becomes 4.96 X101
4.96 X 101 X105 is
4.96 X 106
So
Try
(9.1 X 10-1 ) ( 5.4 X107)
(9.1)(5.4) X 10-1 X 107
So
49.14 X 106 and again 49.14 isn't in scientific notation
changing just 49.14 into scientific notation we get 4.914 X 101
so we have
4.914 X101 X 106
which
is
4.914 X 107
List from least to greatest
3.4 X 10-4 3.4 X 10-5 and 3.4 X 10-6
We noticed that the -6 exponent would be a smaller number-- when we wrote it in standard form so
3.4 X 10-6 < 3.4 X 10-5 < 3.4 X 10-4 would be the listing
Check out the following links:
this one takes you from huge numbers to teeny tiny ones
this one lets you practice scientific notation
this one lets you practice multiplying scientific notation
this one lets you practice dividing sn
this one lets you practice even harder ones!
Math 6A (Periods 1 & 2)
Subtracting Integers 11-3
The life story about someone who was so negative-- you wanted to take a little negativity away but since you can't do that you add a little positiveness-- works in math as well!!
Instead of subtracting ... "ADD THE OPPOSITE!"
We will prove it in class with our little red and yellow tiles... If you need to review, make your own out of red and yellow paper-- or whatever colors you want!!
In life-- to take away a little negative-- add some positive
To take away an integer... add its opposite.
Rule from our textbook
for all integers a and b
a - b = a + (the opposite of b) or
a - b = a + (-b)
Instead of subtracting.. "ADD THE OPPOSITE"
make sure you do the check, check.. you need to have two check marks.. one changing the subtraction to addition and the other changing the sign of the 2nd number to its opposite.
5 - - 2=
5 + + 2= 7
-2 - 5 =
- 2 + - 5 =
before I give you the answer look... we are looking at
-2 + -5
We are adding two negatives.. so we are back to the rules from Section 11-2...
when adding the same sign just add the number and use their sign so
- 2 + - 5 = -7
But what about -2 - -5 ?
adding the opposite, we get
-2 + + 5 .
Now, the signs are different so the rule from Section 11-2 is
ask yourself... "Who wins?" and "By how much?"
Okay, here the positive wins so I know the answer will be +
and by how much means.. to take the difference
5-2 = 3
so -2 + + 5 = +3
Do you need to put the + sign? No, but I like to in the beginning to show that I checked WHO WON!!
What about
-120 - -48?
add the opposite
-120 + + 48 follows the
Different signs rule... so
ask yourself
Who wins? answer: the negative.. so I know the answer will be negative..
And "By How Much?" take the difference 120-48 = 72
so
-120 + + 48 = -72
or
-120 - 48
-120 + (-48) = -168
NEVER EVER CHANGE THE FIRST NUMBER'S SIGN!!
WALK THE LINE, the number line-- that is!!
Remember... Attitude is such a little thing... but it makes a BIG difference!!
Always start with a positive attitude!!
When you walk the line, Which way are you always facing when you start???
Always attempt to get everything into addition so we can follow the rules of Section 11-2 Adding Integers.
1) SAME SIGN rule---> just add the numbers and use their sign
-4 + -5 = -9
2) DIFFERENT SIGNS rule
ask yourself those 2 important questions
a) Who wins? (answer is either negative or positive)
b) By how much? (Take the difference)
Page 376 answers to # 2-18 (evens)
2. -9
4. -5
6. 22
8. -9
10. -74
12. -32
14. -160
16. 498
18. -284
The life story about someone who was so negative-- you wanted to take a little negativity away but since you can't do that you add a little positiveness-- works in math as well!!
Instead of subtracting ... "ADD THE OPPOSITE!"
We will prove it in class with our little red and yellow tiles... If you need to review, make your own out of red and yellow paper-- or whatever colors you want!!
In life-- to take away a little negative-- add some positive
To take away an integer... add its opposite.
Rule from our textbook
for all integers a and b
a - b = a + (the opposite of b) or
a - b = a + (-b)
Instead of subtracting.. "ADD THE OPPOSITE"
make sure you do the check, check.. you need to have two check marks.. one changing the subtraction to addition and the other changing the sign of the 2nd number to its opposite.
5 - - 2=
5 + + 2= 7
-2 - 5 =
- 2 + - 5 =
before I give you the answer look... we are looking at
-2 + -5
We are adding two negatives.. so we are back to the rules from Section 11-2...
when adding the same sign just add the number and use their sign so
- 2 + - 5 = -7
But what about -2 - -5 ?
adding the opposite, we get
-2 + + 5 .
Now, the signs are different so the rule from Section 11-2 is
ask yourself... "Who wins?" and "By how much?"
Okay, here the positive wins so I know the answer will be +
and by how much means.. to take the difference
5-2 = 3
so -2 + + 5 = +3
Do you need to put the + sign? No, but I like to in the beginning to show that I checked WHO WON!!
What about
-120 - -48?
add the opposite
-120 + + 48 follows the
Different signs rule... so
ask yourself
Who wins? answer: the negative.. so I know the answer will be negative..
And "By How Much?" take the difference 120-48 = 72
so
-120 + + 48 = -72
or
-120 - 48
-120 + (-48) = -168
NEVER EVER CHANGE THE FIRST NUMBER'S SIGN!!
WALK THE LINE, the number line-- that is!!
Remember... Attitude is such a little thing... but it makes a BIG difference!!
Always start with a positive attitude!!
When you walk the line, Which way are you always facing when you start???
Always attempt to get everything into addition so we can follow the rules of Section 11-2 Adding Integers.
1) SAME SIGN rule---> just add the numbers and use their sign
-4 + -5 = -9
2) DIFFERENT SIGNS rule
ask yourself those 2 important questions
a) Who wins? (answer is either negative or positive)
b) By how much? (Take the difference)
Page 376 answers to # 2-18 (evens)
2. -9
4. -5
6. 22
8. -9
10. -74
12. -32
14. -160
16. 498
18. -284
Subscribe to:
Comments (Atom)