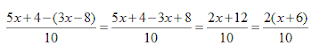Math 6High(Period 3)

Adding Integers Using Addition Rules 4.3

Absolute Value of a number--> is its distance from ZERO on a number line. 

The absolute value of a number a is written as  

The absolute value of any number is always positive because absolute value is a distance concept—and distances are always POSITIVE

When Adding  Integers using the following rules:

To add two integers with the same sign, just add them and use their sign.

To add two integers with different signs, subtract the lesser absolute value from the greater absolute value and write the sign of the integer with the greater absolute value.
We called this  “Who Wins?... and   “ By How Much?”   

That is you decide who is the winner (the integer with the greater absolute value) and you take the difference ( subtract the smaller absolute value from the larger absolute value). Use the “winner’s sign.”

Identity Property of Addition: 

The sum of zero and any integer is the integer

0 + (-3) = -3  

Zero is called the ADDITIVE IDENTITY.

The sum of -3 and -5 is negative because

-3 + -5  are both negative  --> they have the same sign

-3+ -5 = -8

But what about

-5 + 3= ?

These are two integers with DIFFERENT SIGNS… Who wins? The negative… by how much?  5-3 = 2 so the solutions is – 5 + 3 = -2

What about 5 + (-3) ?

Again these are two integers with DIFFERENT SIGNS… Who wins? This time the positive… by how much? 5-3 = 2 so the solutions is  5 +(-3) = 2

Here are a number of good strategies to use when adding more than just two integers….

When adding a series of numbers use the commutative and associative properties of addition to group numbers with the same sign.   

• First, always look for ZERO PAIRS  (they cancel each other out)—giving you less work to do!  
• Find the sum of the positive numbers and the sum of the negative numbers. Then add the two sums.

Finding the average of integers is just the same as finding the average of natural numbers. Just remember to use the strategies above to combine positive and negative numbers.
For instance   The daily temperature for one week in Helene Montana in the winter was 5ºC ,    3ºC,      2ºC,     0ºC,     -2ºC,    -3ºC       -4ºC .   

Notice, there are 7 degrees listed for the 7 days—even though one of them was 0ºC.
You need to make sure you use the 7 temperatures.

In this case I would use zero pairs to add 3 + (-3) and 2 + (-2) and I am left with only adding  5 + (-4) = 1 that was easy.... where is my Easy Button? 

Now divide 1 by the number of temperatures we started with-- that was 7 for the 7 days...

1 /7 is 0.142857…. which would round to a very chilly 0.14ºC

Algebra Honors (Periods 5 & 6)

Adding & Subtracting Fractions  6-5

In chapter 2 Section 9 we reviewed adding and subtracting fractions.

With that we found we could do the reverse….

To add or subtract fractions with the same denominator, you add or subtract their numerators and write that results over the common denominator.

To simplify an expression involving fractions, you write it as a single fraction in simplest form

3c/16 + 5c/16 = 8c/16 = c/2

Be careful when you distribute the subtraction sign to every term in the 2^nd  fraction.

The following really seems simple but many students try to simplify it… BE CAREFUL

 STOP! You can not simplify any farther!

Notice that 3-x = -( x - 3) , the LCD is x – 3

Simplify

You must determine the LCD first. Rewrite the fractions using the LCD of 36

Simplify:

  

Simplify:

Factor completely FIRST

You realize that the LCD is a(a-2)(a+2)

Math 6High ( Period 3)

Adding Integers on a Number Line 4.2

We used the number line to model adding two positive numbers—and we developed a similar pattern for adding integers.  

Please look at our textbook page 171 to see the examples of adding integers—the book uses the color blue to indicate a positive number’s movement along the number line and the color red to indicate movement to the left representing a negative number.

You will discover that

 2 + (-5) = -3

-6 + 8 = 2

Two numbers are opposite if they are the SAME distance from 0 on the number line but are opposite sides of ZERO. 

For example -3 and 3 are opposites because they are both 3 units away from zero.

Again -3 can be read as “the opposite of 3” as well as “negative 3”. 

The expressions –(-3) can be read as “the opposite of negative three”  which would be +3

Inverse Property of Addition
Words: 

The sum of a number and its opposite is zero

Algebraic: 

a + (-a) = 0

Algebra Honors (Periods 5 & 6)

Adding & Subtracting Fractions 
The Least Common Denominator 6-4

We know that we can write a fraction in simpler form by dividing its numerator and denominator by the same nonzero number.

and the reverse is true as well

You can write a fraction in a different form by multiplying the numerator and denominator by the same nonzero number.

3/7 = ?/35

You realize that you multiply 7 by 5 to obtain 35 so you would multiply 3 by 5 to obtain the correct number for the numerator.

3/7 = 15/35

the same applies to fractions with variables…

8/3a = ?/18a²

What do you multiply 3a by to obtain 18a²?   6a

so you must multiply both by 6a    

 Complete:

   

You notice that you need to multiply the denominator by (x +1) so you must do the same to the numerator.

When you add or subtract fractions with different denominators, you will find that using the Least Common Denominator (LCD)  will simplify your work

Find the LCD of:

First factor each denominator completely. Factor Integers into primes!

6x - 30 = 6(x - 5)= 2·3(x - 5)

9x - 45 = 9(x - 5) = 3∙3(x - 5)

Form the product of the greatest power of each
(Remember that the LCM is the product of every factor to its greatest power)

2·3²(x - 5) = 18(x - 5)

Therefore the LCD is 18( x – 5)

Re write the following with their LCD

x² - 8x +16 = (x - 4)²

and

x²- 7x + 12 = (x - 4)(x - 3)

the LCD is (x -4)²(x -3)

Now rewrite each fraction using the LCD

 and

Math 6A (Periods 2 & 4)

Least Common Multiple 5-6
Here is a review of that lesson...
Let’s look at the nonzero multiples of 8 and 12—listed in order
Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72…

Multiples of 12: 12, 24, 36, 48, 60, 72, ….

The numbers 24, 48, and 72, ... are called common multiples of 8 and 12. The least of these multiples is 24 and is therefore called the least common multiple.

LCM(8, 12) = 24

To find the LCM of two whole numbers, we can write out lists of multiples of the two numbers.

Or, we can use prime factorization

Lets find LCM(12, 15)

12 = 2²∙3
15 = 3∙5

The LCM will be made up of the greatest power of each factor

LCM will be 2²∙3∙5 = 60
The book has a third option or method
you can check out, if you’d like

Let’s find LCM (54, 60)


54= 2∙3∙3∙3 = 2∙3³
60 = 2∙2∙3∙5 = 2²∙3∙5

The greatest power of 2 that occurs in either prime factorization is 2²
The greatest power of 3 that occurs in either prime factorization is 3³
The greatest power of 5 that occurs in either prime factorization is 5
Therefore, LCM(54,60) is 2²∙3³∙5 = 540


REMEMBER:
The GCF (greatest common factor) is a factor. The GCF of two numbers will be either the smaller of the two or smaller than both

The LCM (least common multiple) is a multiple. The LCM of the two numbers will be the largest of the two or larger than both.



To find the LCM of two whole numbers you could write out the lists of multiples-- and that works relatively easily with small numbers... but there are more efficient ways to find the least common multiple of two whole numbers.

1. Write out the first few multiples of the larger of the two numbers and test each multiple for divisibility by the smaller number. The first multiple of the larger number that is divisible by the smaller number is the LCM

2. You can use prime factorization to find the LCM. The LCM is EVERY factor to its GREATEST power!!
LCM(54, 60)
54 = 2⋅ 3⋅ 3⋅ 3 = 2⋅ 3³
60 = 2⋅ 2⋅ 3⋅ 5 = 2²⋅ 3⋅ 5
So the greatest power of 2 is 2²
The greatest power of 3 is just 3
and the greatest pwoer of 5 is just 5
so the product of 2²⋅ 3⋅ 5 will be the LCM
LCM(54, 60) = 540

3. You may use the BOX method as shown in class... unfortunately it does not show well here. Remember you need to create a L. The numbers on the side of the box represent the GCF!! You need to multiple them with the last row of factors.
See me before or after class if you want any review!!


We reviewed the concept of relatively prime and noticed that any two prime numbers are relatively prime. We also noticed that if two numbers are relatively prime-- neither of them must be prime....

We also found out that if one number is a factor of a second number, the GCF of the two numbers is the first number AND... if one whole number is a factor of a second whole number the LCM of the two numbers is the second number!!
GCF(12,24) = 12
LCM(12,24) = 24

WOW!!

If two whole numbers are relatively prime---
their GCF = 1
and their LCM is their product!!
GCF(8,9) =1
GCF(8,9) = 72

WOW!!

LCM & GCF Story PRoblems
1) Read the problem
2) Re-read the problem!!
3) Figure out what is being asked for!!
4) find the "magic " word... to help you determine if you are finding GCF or LCM
5) When in doubt... draw it out!!

Math 6 High (Period 3)

Integers & The Number Line 4.1

Integers are the Counting Numbers (also known as Natural Numbers), their opposites, and ZERO.

We have Negative Integers, Positive Integers and Zero. 

The symbol used to represent negative integers is a “negative sign.” 

-4 is normally read as negative 4 

BUT it is also understood to mean “the opposite of 4”

On a number line,
the negative numbers are to the LEFT of ZERO and
the positive numbers are to the RIGHT of ZERO.

Please turn to Page 167 in our textbook and look at the examples of graphing various negative integers on a number line. 

You will notice that -4 is to the left of -1… Therefore -4 < -1  That is -4 IS LESS THAN -1. 

You could also state that -1> -4. That is, -1 IS GREATER THAN -4.

Negative numbers are used in real-life situations to represent sub-zero temperatures as well as losses that occur in business.