Ratios 7-1
The ratio of one number to another is the
quotient when the first number is divided by the second number (and the 2nd
number does not equal 0)
Ratios =
fractions with meaning
A ratio is the comparison of a number a
and a non zero number b using division. The ratio a to b can be written three
ways-- and you read them all the same
1) as a
quotient using the division sign ÷ 1 ÷ 3
3) as a ratio
using a colon 1:3
A ratio of 7
to 4 can be written 7:4 or 7/4
A Ratio needs two numbers. DO NOT make it into a Mixed number!
A Ratio needs two numbers. DO NOT make it into a Mixed number!
32:48 becomes
2:3
You can use ratios to compare 1
quantities of the SAME KIND
To write the ratio of two quantities
of the same kind
1) First express the measures in the
same unit
2) Then write their ratio
Write each ratio in simplest form
3h: 15 min
or 12:1
That’s the same ratio whether you
changed the numerator to minutes or the denominator to hours
9in: 5 ft
Write a ratio of the height of a tree
4m tall to the height of a sapling 50cm tall
1) Express both heights in centimeters
2) Express both heights in meters
When you solve a word problem, you may
need to express a ratio in a different form. If two numbers are in the ratio
3:5 you can use 3x and 5x to represent them, because
The lengths of the sides of a triangle
are in the ratio 3:4:5. The perimeter of the triangle is 24 in. Find the
lengths of each side.
Let the lengths of the sides be 3x,
4x, and 5x
3x + 4x + 5x = 24
12x= 24
x = 2
So the sides of the triangle are 6in,
8 in, and 10 in
Find the ratio of x to y
Collect x-terms on one side and y terms on the other. Then factor
Collect x-terms on one side and y terms on the other. Then factor
3x = 7y
Divide both sides by 3 and then divide
both sides by y
cx –ay = aby - bcx
collecting the x terms on one side and the y terms on the
other you have
cx + bcx = aby + ay
Now factor
x(c + bc) = y( ab + a)
divide both sides by c + bc
then divide both sides by y
you have
BUT… you can still factor
which can simplify to


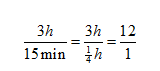





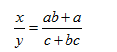
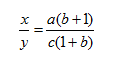

No comments:
Post a Comment