Any common fraction can be written as a decimal by dividing the numerator by the denominator. If the remainder is zero, the decimal is called a terminating, or ending, or finite decimal.
3/8= 0.375
Actually this is one of the fractions you need to know by heart !
If you don’t reach a remainder of zero when dividing the numerator by the denominator, continue to divide until the remainder begins to repeat.
5/6
7/11
The decimal quotient above are nonterminating, nonending, or infinite. The dots indicate that the decimals continue without end.
They are also called repeating or periodic because the same digit or block of digits repeats unendingly. A bar (vinculum) is used to indicate the block of digits that repeat.
What ones do you need to know by heart… same from 6th grade
1/3 family, 1/11 family, and let’s look at the 1/7 family (my favorite)
Let’s look at this algebraically… when you divide a positive integer n by a positive integer d, the remainder r at each step must be zero or a positive integer less than d. For example, if the divisor is 6, the reminders will be 0, 1, 2, 3, 4, or 5 and the division will terminate or begin repeating within 5 steps after only zeros remain to be brought down. Think about this!
For every integer n and every positive integer d, the decimal form of the rational number n/d either terminates or eventually repeats in a block of fewer than d digits.
To express a terminating decimal as a common fraction, express the decimal as a common fraction with a power of ten as the denominator. Then express in simplest form
To express a repeating decimal follow these steps :
You should get 179/330
This one can be done easily if you remember the rule of matching the block of repeating digits with the digits in the decimal.
In this case
All terminating and all repeating decimals represent rational numbers that can be written in the form n/d where n is an integer and d is a positive integer.
It is often convenient or even required that you use an approximation of a lengthy decimal. For example, you may approximate 7/13 as 0.53846, or 0.538, or 0.54
As review: to round a decimal
1. if the first digit dropped is greater than or equal to 5, add a 1 to the last digit retained.
2. if the first digit dropped is less than 5, don’t change the last digit retained
Use the symbol ≈ which means “is approximately equal to”
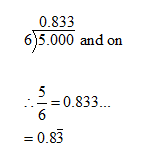






No comments:
Post a Comment