Rational Square Roots 11-3
You know that subtraction undoes addition, and that division by a nonzero number undoes multiplication, Similarly squaring a number can be undone by finding a square root.
If a2 =b then a is a square root of b
Notice that 72= 49 and so does (-7)2 = 49 So 7 and -7 are square roots of 49
the radical symbol √ is used to write the principal or positive square root of a positive number.
is read “The positive square root of 49 equals 7
A negative square root is associated with the symbol - √
is read “The negative square root of 49 equals -7”
Let’s use ± to indicate both the positive (also called the principal) square root and negative square root so
means the positive or negative square root of 49 or ±7
Let’s look at
the number written beneath the radical sign (such as 49) is called the radicand.
For all positive real numbers a:
Every positive real number a has two square roots
Every positive real number a has two square roots
The symbol
denotes the principal square root of a
Zero has only one square root—itself.
Because the square of every real number is either positive or zero—>NEGATIVE NUMBERS DO NOT HAVE SQUARE ROOTS IN THE SET OF REAL NUMBERS.
does not have a solution in the set of real numbers!!
Notice that
and that
so...
Product Property of Square RootsFor any non-negative real numbers a and b,
Find:
Let’s say you forgot your perfect squares—OH MY!!
but looking at 225, using your skills from previous years you realize 225 = 9 · 25 so
If you cannot see any perfect squares that divide the radicand—begin by factoring it!! Then see if you have any perfect squares. USE INVERTED DIVISION!!
Always use PERFECT SQUARES when using inverted division. We practiced in class.
Use inverted division along with divisibility rules to find perfect squares Look for the largest perfect square factors ... and you discover that
Quotient Property of Square Roots
For any non negative real number a and any positive real number:
Find the indicated square root
2nd day: If you don’t see any perfect squares—especially with numbers like these—simplify your fraction first
and that's easy to do... it is 2/5
What about
Express as a decimal first then it should become easier
Let’s look at






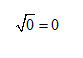















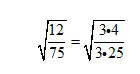




No comments:
Post a Comment