Math 6A ( Periods 1 & 2)

Multiplying Fractions 2-1

A park has a playground that is ¾  of its width  and ⅘ of its length. What fraction of the park is the playground?

In class, fold a piece of paper  horizontally into fourths and shade three of the four sections (yellow) to represent ¾

Fold the paper vertically into fifths and shade ⅘ of the paper blue!

COUNT the total number of squares. This number is the denominator. The numerator is he number number of squares shaded with both colors!

34 4 5=12 20=35  So the playground covers ⅗ of the entire park!

KEY IDEA:  Multiplying Fractions

Words: Multiply the numerators and then multiply the denominators.

Number Example:  

Algebra:  where b and d are both not equal to ZERO!

Find     Notice you multiply the numerators first, then multiply the denominators

When the numerator of one fraction is the SAME as the denominator of another fraction, you can use mental math to multiply For example: 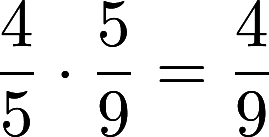 because you can divide out the common factor 5.

Find         

Using what we know we would do the following     

    

But could we simply before we multiply?  YES!!

Divide out Common Factors FIRST

Looking at 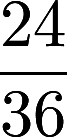  What do you notice?  The GCF( 24, 36)  = 12. We will be using the GCF of numbers to simplify our fractions!  

KEY IDEA: Multiplying Mixed Numbers

Write each mixed number as an improper fraction. Then multiply as you would with fractions

Find                       Write as the improper fraction

Now rewrite the problem

Now, I want you to get comfortable with both the improper fraction and the mixed number, so practice giving both forms as your solution!  In Algebra there are many times when you will be leaving your number as an improper fraction!

Find    Write both Mixed Numbers as improper fractions

NOTE: Before you start multiplying the numerators check to see if you can simplify BEFORE you begin!  I see something… do you?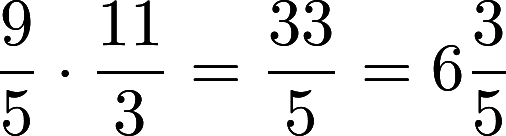

Is this a reasonable answer?  Why?