Graphing Quadratic Functions 9-1
The standard form of a quadratic ( 2nd degree function) is
ax2 + bx + c
The shape it makes when you graph it is called a parabola
Parabolas are symmetric around a line called the axis of symmetry. (AoS)
The axis goes through a point on the parabola called the vertex
The vertex is the maximum if the graph is a sad face and a minimum if it’s a happy face.
The parent graph is the simplest form of the graph.
For quadratics, the parent graph is y = x2
Note: that while b and c can both be ZERO, “a” can NEVER be zero for a quadratic.
WHY? Then it would be a linear equation.
if a > 0 ( positive) the parabola opens upward ( happy face)
if a < 0 ( negative) the parabola opens downward ( sad face)
What happens as the “a” coefficient gets really big or really small ( fraction / decimal)?
The larger the “a” coefficientà the narrower the parabola.
The smaller (fractional/decimal) the “a” coefficientà the wider the parabola
{THINK: what happened when the “m” (or slope) coefficient got big? The slope got steeper. So, similarly, both sides of the U get steeper at the same time!!}
{NOW THINK: what
happened when the “m” (or slope) coefficient got tiny ( or fractional)? The
slope became what we called a bunny slope. So, similarly, both sides of the U
get to be bunny slopes at the same time!!}
The x value of the vertex as well as the axis of symmetry are the SAME:
a and be are from the standard form of the quadratic.
Notice when b is missing ( b = 0), the vertex is always on the y-axis!! and therefore the axis of symmetry ( AoS) is also the y-axis.
The c value is the y-intercept ( when b=0) because when x = 0 you are on the y axis.
f(x) = ax2 + bx+ c
f(0) = a(0)2 + b(0) + c
f(0) = c = the y value … and in this case the y-intercept!
The domain of
a quadratic (parabola) that is a function (opens up or down) is ALL REAL
NUMBERS
The range depends on which way it opens:
If it opens up, the range will be

If it opens down, the range will be
The range depends on which way it opens:
If it opens up, the range will be

If it opens down, the range will be
You can graph quadratics exactly the same way you graphed lines—plug in your choice of an x value and use the equation to find your y value
Because it is a U shape, you should graph at least 5 points as follows:
FIRST: make sure the equation is in standard form!
y must be isolated on one side and then you can read the a and b coefficients
y must be isolated on one side and then you can read the a and b coefficients
y = ax2
+ bx + c
Point 1) the vertex: the
minimum value of the smile or the maximum value of the frown
the x value of the VERTEX is -b/2a
Plug that into the equation and find the y value of the vertex
Next draw the AXIS OF SYMMETRY (AoS)
the x value of the VERTEX is -b/2a
Plug that into the equation and find the y value of the vertex
Next draw the AXIS OF SYMMETRY (AoS)
Notice- this is a linear equation! It is a line through the vertex that is parallel to the y-axis!
Point 2) Pick an x value immediately to the right or the left of the AXIS OF SYMMETRY (AoS) and find its “y” by plugging into the equation.
Point 3) Pick another x value one step farther on that same side of the AXIS OF SYMMETRY (AoS) as point 2—and find its “y” by plugging into the equation.
Points 4 and 5) Graph the mirror image of both Point 2 and Point 3 on the other side of the AXIS OF SYMMETRY (AoS) by counting from the of the AXIS OF SYMMETRY (AoS)
You can choose to do two more points—if you want—but your points are joined in a SMOOTH U SHAPE ( not a V shape) and extend the lines with arrows on each end!
Notice right away—the “a” coefficient is negative so this is a frown face… a sad face! You know which way the graph will open! (Downward)
The x value of the vertex is –b/2a a = -3 but b = 0 ( it is missing!)
so the x value of the vertex is –b/2a = -0/2(-3) = 0 Plug that back into the function f(0) = -3(02) = 0
(Or just begin to
realize that if b is missing the vertex is always on the y axis and the AXIS
OF SYMMETRY (AoS) will always be x = 0. )
In this case because there is NOT a “c” in the function, the vertex is ( 0,0) the origin.
The domain is all real numbers
1) Graph the
vertex ( 0,0)
2) Draw the AXIS OF SYMMETRY (AoS) a dotted line at x = 0 ( actually this is the y-axis so use a different colored pencil to indicate the AoS)
3) Pick an x value immediately to the right of the AoS, x = 1 works so plug that into the equation to find its y value
y = -3(12) = -3 PLOT ( 1, -3)
4) Pick the next x value x = 2 and plug that into the equation to find its y value
y = -3(22) = -12 PLOT ( 2, -12)
5) Count the same 1 step to the LEFT of the AoS as at the same y value of ( 1, -3) That would be ( -1, -3) and plot that point!
6) Count the same 2 steps to the LEFT of the AoS at the same y value of ( 2 -12) That would be ( -2, -12) and plot that point
7) Connect with a smooth U shape and extend with arrows!

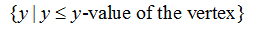



No comments:
Post a Comment