Thursday, March 14, 2013
Algebra Honors ( Periods 5 & 6)
Graphs of Quadratic Equations: The Discriminant 12-4
Sometimes it is NOT necessary to draw the graph of an equation.
Knowing the relationships between an equation and its graph— you can obtain important information from the equation itself.
Today’s lesson illustrates the relationship between the number of roots of a quadratic equation and the number of x-intercepts of the related parabola.
In the parabola the x coordinate of a point where the curve intersects the x axis is called an x-intercept of the curve.
Looking at the parabola on page 572 you notice that this parabola has two x-intercepts, -1 and 3 because y = 0 for both of these values of x.
you can also see that
x2- 2x – 3 = 0 or (x +1)(x-3) = 0
has -1 and 3 as its roots, solutions, zeros… {-1,3}
The algebraic fact that a quadratic equation can have two, one or no real number roots corresponds to the fact that a parabola can have two, one or no x-intercepts…
and we can find that out by just working with the quadratic equations—rather than having to graph…
However… let’s graph a few
Example 1: x2 + 4x + 1 = 0
find –b/2a
-4/2 = -2
f(-2) = (-2)2 + 4(-2) + 1 = 4 -8 + 1 = -3
so (-2,-3) is the vertex
x = -2 is the axis of symmetry
Create an x y table
f(-1) = (-1)2 +4(-1) + 1 = 1 -4 +1 = -2
f(0) = 02 + 4(0) + 1 = 1
x y
-1 -2
0 1
Now solve
Solving x2 + 4x + 1 = 0
Now graph
Number of roots: two real roots Number of x-intercepts: two
Example 2 : x2 + 2x + 1 = 0
find -b/2a -2/2 = -1
f(-1) = (-1)2 + 2(-1) + 1 = 1 -2 + 1 = 0
(-1.0) is the vertex
and x = -1 is the axis of symmetry
create an xy table
f(0)=02 + 2(0) + 1 = 1
f(1) = (1)2 +2(1) + 1 = 4
x y
0 1
1 4
Now graph
Now Solve
Solving x2 + 2x + 1 = 0
We can solve easily but let’s use the quadratic formula
= -1
The solution set is {-1}
Number of roots: 1 real root Number of x- intercepts: one
Example 3: x2 -4x + 7 = 0
find –b/2a= +4/2 = 2
f(2) = (2)2 -4(2) + 7 = 4 -8 + 7 = 3
vertex ( 2, 3)
and x= 2 is the axis of symmetry
create an xy table
f(1) = (1)2 -4(1) + 7
f(0) = (0)2 -4(0) + 7
x y
1 4
0 7
Now graph
Now solve
x2 -4x + 7 = 0
There is NO REAL number root since does not represent a real number
Number of roots: no real number roots Number of x intercepts: None
In each of these examples the value of b2-4ac in the quadratic formula is the key to the number of real roots.
When b2-4ac is negative, there is no real number root of the equation ax2 + bx + c = 0 because square roots of negative numbers do not exist in the set of real numbers.
Because the value of b2-4ac discriminates, or points out differences, among these 3 cases above, it is called the discriminant of the quadratic equation.
The discriminant is only part of the quadratic formula and simpliy helps one determine the number of roots.
If b2-4ac < 0 "no real roots"
If b2-4ac = 0 "one rational root"
If b2-4ac > 0 " two real roots" we can break this down even more specific:
If b2-4ac is a perfect square then " two rational roots"
If b2-4ac is a non-square then "two irrational roots"
Subscribe to:
Post Comments (Atom)
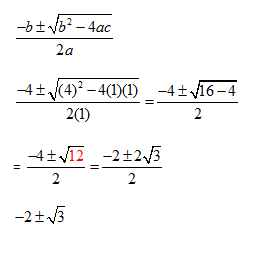



No comments:
Post a Comment