Adding & Subtracting Fractions:
The Least Common Denominator 6-4
The Least Common Denominator 6-4
We know that we can write a fraction in simpler form by
dividing its numerator and denominator by the same nonzero number.
and the reverse is true as well
You can write a fraction in a different form by multiplying
the numerator and denominator by the same nonzero number.
3/7 = ?/35
You realize that you multiply 7 by 5 to obtain 35 so you would
multiply 3 by 5 to obtain the correct number for the numerator.
3/7 = 15/35
the same applies to fractions with variables…
8/3a = ?/18a2
What do you multiply 3a by to obtain 18a2? 6a
so you must multiply both by 6a
Complete:
You notice that you need to multiply the denominator by (x +1)
so you must do the same to the numerator.
When you add or subtract fractions with different
denominators, you will find that using the Least Common Denominator (LCD) will simplify your work
Find the LCD of:
First factor each denominator completely. Factor Integers into
primes!
6x-30 = 6(x - 5)= 2·3(x - 5)
9x -45 = 9(x - 5) = 3∙3(x - 5)
Form the product of the greatest power of each
(Remember that the LCM is the product of every factor to its greatest power)
(Remember that the LCM is the product of every factor to its greatest power)
2·32(x - 5) = 18(x - 5)
Therefore the LCD is 18( x – 5)
Re write the following with their LCD
x2- 8x +16 = (x - 4)2
and
x2- 7x + 12 = (x - 4)(x - 3)
the LCD is (x -4)2(x -3)
Now rewrite each fraction using the LCD
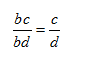





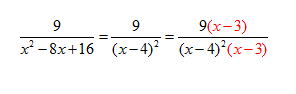
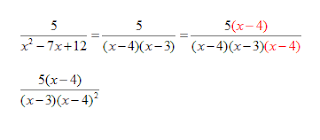
No comments:
Post a Comment