Ratios 6-1
In one of our our textbook, the example given involves the number of students --at what I called a mythical middle school --as well as the number of teachers. There are 35 teachers and 525 students. We can compare the number of teachers to the number of students by writing a quotient
35
525
1/15
The quotient of one number divided by a second number is called the ratio of the first number to the second number.
We can write a ratio in the following ways:
1/15 1:15 1 to 15
All of these expressions are read one to fifteen.
If the colon notation is used the first number is divided by the second. A ratio is said to be lowest terms if the two numbers are “relatively prime.”
You do not change an improper fraction to a mixed number if the improper fraction represents a ratio
There are 9 players on a baseball team. Four of these are infielders and 3 are outfielders. Find each ratio in lowest terms.
a. infielders to outfielders
b. outfields to total players
# of infielders
# of outfielders
= 4/3 or 4:3 or 4 to 3
# of outfielders
# total of players
= 3/9 = 1/3 or 1:3 or 1 to 3
A baseball players batting average is the ratio of the number of hits to the number of office times at bat.
Example is Nomar Garciaparr who got 190 hits in his 523 times at bat.
190/5332 = 5/14
Normally, batting averages are given as decimals rounded to the nearest thousandths. But we can write this ratio as 5:14 or as " 5 to 14."
We then compares two ratios. We looked at two different fish tanks
tank A had 2 fish in it and was 40 quarts
Tank B had 3 fish in it and was 15 gallons
Fish in Tank A 2 fish
Fish in Tank B 3 fish
2
3
Volume in Tank A
Volume in Tank B
40 quarts
15 gallons
WAIT-- we must compare quantities in terms of common units. When a common unit is used, the ratio a:b does NOT have units!
4 quarts = 1 gallon so 40 quarts must be 10 gallons
10 gallons
15 gallons
10/15 = 2/3
The two ratios are equal
Comparing Three Ratios
We compared the records of three soccer teams from three different schools
Chestnut HS wins: 10 AND losses: 8
Mae Jennison wins: 12 AND losses: 8
Buena Vista wins: 16 AND losses: 12
Which team had the best record?
Two Methods:
A. Find the team with the greatest ratio of wins to losses
Chestnut : 10/8 = 5/4
Mae Jennison: 12/8 = 3/2
Buena Vista: 4/3
Mae Jennison has the best record
B. Find the team with the greatest ratio of wins to TOTAL games:
Chestnut: 10/18 = 5/9
Mae Jennison: 12/20 = 3/5
Buena Vista: 16/28 = 4/7
Because 3/5= 0.6 is greater than 5/9 (5/9= 0.55555) or 4/7( 4/7= 0.5714...)
Mae Jennison has the best record
Notice we change the fractions to decimals to compare. However, you can use your skills with fractions to easily compare the fractions.
A baseball players batting average is the ratio of the number of hits to the number of office times at bat.
Example is Nomar Garciaparr who got 190 hits in his 523 times at bat.
190/5332 = 5/14
Normally, batting averages are given as decimals rounded to the nearest thousandths. But we can write this ratio as 5:14 or as " 5 to 14."
We then compares two ratios. We looked at two different fish tanks
tank A had 2 fish in it and was 40 quarts
Tank B had 3 fish in it and was 15 gallons
Fish in Tank A 2 fish
Fish in Tank B 3 fish
2
3
Volume in Tank A
Volume in Tank B
40 quarts
15 gallons
WAIT-- we must compare quantities in terms of common units. When a common unit is used, the ratio a:b does NOT have units!
4 quarts = 1 gallon so 40 quarts must be 10 gallons
10 gallons
15 gallons
10/15 = 2/3
The two ratios are equal
Comparing Three Ratios
We compared the records of three soccer teams from three different schools
Chestnut HS wins: 10 AND losses: 8
Mae Jennison wins: 12 AND losses: 8
Buena Vista wins: 16 AND losses: 12
Which team had the best record?
Two Methods:
A. Find the team with the greatest ratio of wins to losses
Chestnut : 10/8 = 5/4
Mae Jennison: 12/8 = 3/2
Buena Vista: 4/3
Mae Jennison has the best record
B. Find the team with the greatest ratio of wins to TOTAL games:
Chestnut: 10/18 = 5/9
Mae Jennison: 12/20 = 3/5
Buena Vista: 16/28 = 4/7
Because 3/5= 0.6 is greater than 5/9 (5/9= 0.55555) or 4/7( 4/7= 0.5714...)
Mae Jennison has the best record
Notice we change the fractions to decimals to compare. However, you can use your skills with fractions to easily compare the fractions.
Some ratios compare measurements. In these cases we must be sure the measurements are expressed in the same units
It takes Matt 4 minutes to mix some paint for his science project. It takes him 3 hours to complete painting his science project. What is the ratio of the time it takes Matt to mix the paint to the time it takes Matt to paint his project?
Use minutes as a common unit for measuring time. You must convert the hours to minutes first
3h = 3 · 60min = 180 min
The ratio is :
min to mix
min to paint
= 4/180 = 1/45 or 1:45
Some ratios are in the form
40 miles per hour or 5 pencils for a dollar
“ I want my… I want my…. I want my … MPG!!”
These ratios involve quantities of different kinds and are called rates. Rates may be expressed as decimals or mixed numbers. Rates should be simplified to a per unit form. When a rate is expressed in a per unit form, such a rate is often called a unit rate.
Amir’s dad’s car went 258 miles on 12 gallons of gas. Express the rate of fuel consumption in miles per gallon.
The rate of fuel consumption is
258 miles
12 gallons
= 21 1/2 miles per gallon
Some of the most common units in which rates are given are the following:
mi/gal or mpg miles per gallon
mi/h or mph miles per hour
km/L kilometers per liter
km/h kilometers per hour
Page 229
1 What is the cost of grapes in dollars per kilogram if 4.5 kg of grapes costs $7.56?
$7.56/4.5 kg divide carefully and you discover it is $1.68/kg
2. THe index of refraction of a transparent substance is the ratio of the speed of light in space to the speed of light in the substance.
Using the table from the textbook (look at page 229) Find the index of refraction of
a) glass
300,000/200,000 straight from the chart, which can simplify to 3/2
b) water
300,000/225,000 again from the chart, which can simplify to 4/3
3. The mechanical advantage of a simple machine is the ratio of the weight lifted by the machine to the forse necessary to lift it.
What is the mechanical advantage of a jack that lifts a 3200 pound car with a force of 120 pounds?
3200/120 = 80/3
4. The C string of a cello vibrates 654 times in 5 seconds. How many vibrations per second is this?
654 vibrations/5seconds... divide carefully and you find... 130 4/5 vibrations per second
5. A four-cubic-foot volume of water at sea level weights 250 pounds. What is the density of water in pound per cubic foot?
250 pounds/4 cubic ft ... divide carefully and you find 62 1/2 lb/ft3
6. A share of stock that costs $88 earned $16 last year. What was the price to earnings ratio?
88/16 = 11/2
7. we did in our spiral notebooks this year... please check
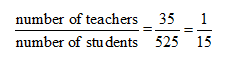

No comments:
Post a Comment