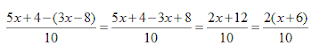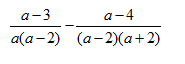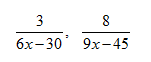Math 6A ( Periods 2 & 4)

Fractions & Mixed Numbers 6-3

1/2 + 1/2 + 1/2 = 3/2

A fraction whose numerator is greater than or equal to its denominator is called an improper fraction.
Every improper fractions is greater than 1
A proper fraction is a fraction whose numerator is less than its denominator.
Thus, a proper fraction is always between 0 and 1

1/4, 2/3, 5/9. 10/12 17/18 are all proper fractions

5/2, 8/3, 18/15, 12/5 are all improper fractions

You can express any improper fraction as the sum of a whole number and a fraction
a number such as 1 1/2 is called a mixed number

If the fractional part of a mixed number is a proper fraction in lowest terms, the mixed number is said to be in simple form.

To change an improper fraction into a mixed number in simple form, divide the numerator by the denominator and express the remainder as a fraction.
14/3 = 4 2/3
30/4 = 7 2/4 = 7 1/2

To change a mixed number to an improper fraction rewrite the whole number part as a fraction with the same denominator as the fraction part and add together.

or multiply the denominator by the whole number part and add the fractional part to that...
In class I showed the circle shortcut. If you were absent, check with a friend or ask me in class!!

2 5/6 =

(2 x 6) + 5
6
=17/6


Practice these:

785 ÷ 3

852÷ 5

3751÷ 16

98001÷231


post your answers below in the comments for extra credit !!

Math 6 High (Period 3)

Dividing Integers 4.6

According to your textbook, a useful way to divide integer  is to think of it as a multiplication problem. that is, when you consider   -15  ÷ 3  =?  rethink it as  3 · ? = -15.  

You know that  (3)(-5) = -15  so you can conclude that -15  ÷ 3  = -5   

Use similar reasoning for other division problems!

More generally, when dividing two integers, divide their absolute values and then use the same rules applied to multiplying integers:

Specifically:

The quotient of two positive integers is positive

The quotient of two negative integers is positive

The quotient of two integers with different signs is negative

The quotient of 0 and a non-zero integer is 0.

Note: an expression with 0 in the divisor  such as 4 ÷ 0 is undefined. You cannot divide  a number by 0.

Evaluating an expression such as   -18/x 

a) when x = -3

1.  First substitute in using parentheses for the number     -18/(-3)

2.  Then DO THE MATH  remembering that the quotient of two negative numbers is positive. 

3.  The solution is +6.

b) when x = 3

1. First substitute in using parentheses for the number   -18/(3)

2. Then DO THE MATH remembering that the quotient of two integers with different signs is always negative.   

3. The solution is -6.

Finding an Average With Integers

To find the average,   always add the numbers first.

The example in the book uses the following measurements (in feet) taken from the bottom of Lake Michigan and find the average lake bottom’s elevation to its surface….

-844,  -865, - 900,  -893,  -888

so to add do the following

-844 + (-865) + (-900) +(-893) + (-888)

Now, I recommend stacking them to add carefully.  

Remembering the rule for adding integers—when adding integers with the SAME sign, just add them and USE THEIR sign… so we know the total must still be negative since they are ALL negative… and we get – 4390

Now, there are 5 numbers so we divide by +5   

            -4390/5

We see that we have a negative divided by a positive.  

We know our quotient will be negative

-4390/5 = -878

So  the average of the lake’s bottom elevation is -878 feet or you could state it is 878 feet BELOW the lake surface.

Math 6 High (Period 3)

Multiplying Integers 4.5 

As we discovered any number multiplied by -1  is equal to its opposite.

-1 ∙ a = -a

We use this Multiplicative Property of -1  to develop general rules for multiplying integers.

 Specifically:

The product of two positive integers is positive

The product of two negative integers is positive

The product of two integers with different signs is negative

The product  of 0 and a non-zero integer is 0.

Examples

Multiplying Integers with the same sign:

(4)(7) = 28

(-11)(-4) = +44

Multiplying Integers with different  signs:

(5)(-5) = -25

(-8)(9) = -72

Evaluating an expression such as:

a)   x y     when x = -15 and y = -6

1.  First substitute in using parentheses for the numbers     (-15)(-6)

2.  Then DO THE MATH  remembering that the product of two negative numbers is positive. 

3.  The solution is +90.

b) ( -a)(b) when a = -4 and b = -8 

(Be careful with these types—they can be tricky)

1. First substitute in using parentheses for the number   -(-4)(-8)

2. Now look at –(-4) first  that really says to take the opposite of -4 and we know that the opposite of -4 is 4 so we really have (4)(-8)

3. Then DO THE MATH remembering that the product of two integers with different signs is always negative.   

4. The solution is -32.

Multiplying Three or MORE  Integers

The following is our textbooks instructions:

• To multiply three or more integers work from left to right, multiplying two numbers at a time.
•   Find the product of the first two numbers, the multiply that product by the next number to the right
•      Continue until all numbers have been multiplied to find the final product.

EXAMPLES:

(2)(-3)(4)  = (-6)(4) = -24

(-4)(5)(0) = (-20(0) = 0 

My Note:  But why even do the multiplication? Any number  multiplied by 0 is 0 so you know right away the solution is ZERO!!!

(-1)(-2)(-3)(-4) = (2)(-3)(-4) = (-6)(-4) = 24

We discussed in class to be a sign counter—If the number of negative signs (in your non-zero multiplication problem) is EVEN then your solution will be POSITIVE. If the number is ODD, then your solution will be NEGATIVE.  The sign of the product depends on the number of factors (assuming all are non-zero) that are negative.

The product of two integers with the same sign is POSITIVE

    The product of two integers with different signs is NEGATIVE

Math 6A (Periods 2 & 4)

Equivalent Fractions 6-2


We drew the four number lines from Page 182 and noticed that 1/2, 2/4, 3/6, and 4/8 all were at the midpoints of the segment from 0 to 1. They all denoted the same number and are called equivalent fractions.

If you multiply the numerator and the denominator by the same number the results will be a fraction that is equivalent to the original fraction

1/2 = 1 x 3/2 x 3 = 3/6

It works for division as well
4/8 = 4 ÷ 4 / 4 ÷ 8 = 1/2

So we can generalize and see the following properties
For any whole numbers a, b, c, with b not equal to zero and c not equal to zero

a/b = a x c/ b x c and
a/b = a ÷ c / b ÷c


Find a fraction equivalent to 2/3 with a denominator of 12
we want a number such that 2/3 = n/12
You could look at this and say
" What do I do to 3 to get it to be 12?
Multiply by 4
so you multiply 2 by 4 and get 8 so
8/12 is an equivalent fraction


A fraction is in lowest terms if its numerator and denominator are relatively prime-- That is if their GCF is 1

3/4, 2/7, and 3/5 are in lowest terms.
They are simplified
You can write a fraction in lowest terms by dividing the numerator and denominator by their GCF.


Write 12/18 is lowest terms
The GCF (12 and 18) = 6

so 12/18 = 12÷ 6 / 18 ÷ 6 = 2/3

Find two fractions with the same denominator that are equivalent to 7/8 and 5/12
This time you need to find the least common multiple of the denominators!! or the LCD
Using the box method from Chapter 5, we find that the LCM (8, 12 ) = 24

7/8 = 7 X 3 / 8 X 3 = 21/24
and
5/12 = 5 X 2 / 12 X 2 = 10/24


When finding equations such as
3/5 = n/15 we noticed we could multiply the numerator of the first fraction by the denominator of the second fraction and set that equal to the denominator of the first fraction times the numerator of the second... or

3(15) = 5n now we have a one step equation

If we divide both sides by 5 we can isolate the variable n and solve...
3(15)/ 5 = n
9 = n

We found we could generalize

If a/b = c/d then ad = bc

Math 6A (Periods 2 & 4)

Fractions 6-1

The symbol 1/4 can mean several things:
1) It means one divided by four
2) It represents one out of four equal parts
3) It is a number that has a position on a number line.

1/8 means 1 divided by 8 or 1 ÷ 8
A fraction consists of two numbers
The denominator tells the number of equal parts into which the whole has been divided.
The numerator tells how many of these parts are being considered.
we noted that we could abbreviate ...

denominator as
denom with a line above it

and numerator as numer

we found that you could add

1/3 + 1/3 + 1/3 = 3/3 = 1
or 1/4 + 1/4 + 1/4 + 1/4 = 4/4 = 1
we also noted that 8 X 1/8 = 8/8 = 1

We also noticed that 2/7 X 3 = 6/7


So we discussed the properties
For any whole numbers a, b,and c with b not equal to zero

1/b + 1/b + 1/b ... + 1/b = b/b = 1 for b numbers added together

and we noticed that b ∙  1/b = b/b = 1
we also noticed that

(a/b) ∙ c = ac/b

We talked about the parking lot problem on Page 180

A count of cars and trucks was taken at a parking lot on several different days. For each count, give the fraction of the total vehicles represented by
(a) cars
(b) trucks

Given: 8 cars and 7 trucks
We noticed that you needed to find the total vehicles or 8 + 7 = 15 vehicles

(a) fraction represented by cars is 8/15
(b) fraction represented by trucks is 7/15

What if the given was: 12 trucks and 15 cars

(a) fraction represented by cars is 15/27
(b) fraction represented by trucks is 12/27

What about
GIVEN:
9 cars and    35 vehicles
This time we need to find out how many trucks there are
35 - 9 = 26
so
(a) 9/35
(b) 26/35

We aren't simplifying YET

Math 6High (Period 3)

Subtracting Integers 4.4

So to generalize the rules we discussed in class, when using a number line to show subtraction (Looking at Page 181 at the number line examples):

To subtract a positive integer , move in the negative direction

To subtract a negative integer, move in the positive direction.

ADD The Opposite!
We had a huge discussion about way too pessimistic people and how we wish we could take away a little of their negativity… and  about too positive people—even someone in our class [ :) ] whom some of us  wished was just a little less positive!! We talked about how instead of taking away a little – if we gave a little of the opposite—that might work as well… and we realized that this applies to math as well.

ADD THE OPPOSITE

That is, instead of subtracting a number—add it’s opposite. 

Then use the rules for adding integers that you have learned from the previous lessons

In general:    a - b = a + (-b)

Several examples:

6 – 8 = 6 + (-8)  In this case by adding the opposite, you are adding two integers with different signs—so you following the adding integers with DIFFERENT SIGNS RULE. Ask “Who wins?” and “by how much?”  The negative wins by 2 so the answer is -2              

6-8 = -2

-9 - 10 =  -9 + (-10) In this case you are adding two integers with the same sign. So use the SAME SIGN RULE.  -9 + (-10) = -19

What about

54- (-12) = 54 + (+12) = 54 + 12  In this case you are adding two integers with the same sign. So use the SAME SIGN RULE.  54 –(-12) = 66

We talked about  making sure to double check—that is, check, check—both  places- where you change the subtraction sign to a positive AND where you change the second numbers sign to its opposite.  

Math 6High(Period 3)

Adding Integers Using Addition Rules 4.3

Absolute Value of a number--> is its distance from ZERO on a number line. 

The absolute value of a number a is written as  

The absolute value of any number is always positive because absolute value is a distance concept—and distances are always POSITIVE

When Adding  Integers using the following rules:

To add two integers with the same sign, just add them and use their sign.

To add two integers with different signs, subtract the lesser absolute value from the greater absolute value and write the sign of the integer with the greater absolute value.
We called this  “Who Wins?... and   “ By How Much?”   

That is you decide who is the winner (the integer with the greater absolute value) and you take the difference ( subtract the smaller absolute value from the larger absolute value). Use the “winner’s sign.”

Identity Property of Addition: 

The sum of zero and any integer is the integer

0 + (-3) = -3  

Zero is called the ADDITIVE IDENTITY.

The sum of -3 and -5 is negative because

-3 + -5  are both negative  --> they have the same sign

-3+ -5 = -8

But what about

-5 + 3= ?

These are two integers with DIFFERENT SIGNS… Who wins? The negative… by how much?  5-3 = 2 so the solutions is – 5 + 3 = -2

What about 5 + (-3) ?

Again these are two integers with DIFFERENT SIGNS… Who wins? This time the positive… by how much? 5-3 = 2 so the solutions is  5 +(-3) = 2

Here are a number of good strategies to use when adding more than just two integers….

When adding a series of numbers use the commutative and associative properties of addition to group numbers with the same sign.   

• First, always look for ZERO PAIRS  (they cancel each other out)—giving you less work to do!  
• Find the sum of the positive numbers and the sum of the negative numbers. Then add the two sums.

Finding the average of integers is just the same as finding the average of natural numbers. Just remember to use the strategies above to combine positive and negative numbers.
For instance   The daily temperature for one week in Helene Montana in the winter was 5ºC ,    3ºC,      2ºC,     0ºC,     -2ºC,    -3ºC       -4ºC .   

Notice, there are 7 degrees listed for the 7 days—even though one of them was 0ºC.
You need to make sure you use the 7 temperatures.

In this case I would use zero pairs to add 3 + (-3) and 2 + (-2) and I am left with only adding  5 + (-4) = 1 that was easy.... where is my Easy Button? 

Now divide 1 by the number of temperatures we started with-- that was 7 for the 7 days...

1 /7 is 0.142857…. which would round to a very chilly 0.14ºC

Algebra Honors (Periods 5 & 6)

Adding & Subtracting Fractions  6-5

In chapter 2 Section 9 we reviewed adding and subtracting fractions.

With that we found we could do the reverse….

To add or subtract fractions with the same denominator, you add or subtract their numerators and write that results over the common denominator.

To simplify an expression involving fractions, you write it as a single fraction in simplest form

3c/16 + 5c/16 = 8c/16 = c/2

Be careful when you distribute the subtraction sign to every term in the 2^nd  fraction.

The following really seems simple but many students try to simplify it… BE CAREFUL

 STOP! You can not simplify any farther!

Notice that 3-x = -( x - 3) , the LCD is x – 3

Simplify

You must determine the LCD first. Rewrite the fractions using the LCD of 36

Simplify:

  

Simplify:

Factor completely FIRST

You realize that the LCD is a(a-2)(a+2)

Math 6High ( Period 3)

Adding Integers on a Number Line 4.2

We used the number line to model adding two positive numbers—and we developed a similar pattern for adding integers.  

Please look at our textbook page 171 to see the examples of adding integers—the book uses the color blue to indicate a positive number’s movement along the number line and the color red to indicate movement to the left representing a negative number.

You will discover that

 2 + (-5) = -3

-6 + 8 = 2

Two numbers are opposite if they are the SAME distance from 0 on the number line but are opposite sides of ZERO. 

For example -3 and 3 are opposites because they are both 3 units away from zero.

Again -3 can be read as “the opposite of 3” as well as “negative 3”. 

The expressions –(-3) can be read as “the opposite of negative three”  which would be +3

Inverse Property of Addition
Words: 

The sum of a number and its opposite is zero

Algebraic: 

a + (-a) = 0

Algebra Honors (Periods 5 & 6)

Adding & Subtracting Fractions 
The Least Common Denominator 6-4

We know that we can write a fraction in simpler form by dividing its numerator and denominator by the same nonzero number.

and the reverse is true as well

You can write a fraction in a different form by multiplying the numerator and denominator by the same nonzero number.

3/7 = ?/35

You realize that you multiply 7 by 5 to obtain 35 so you would multiply 3 by 5 to obtain the correct number for the numerator.

3/7 = 15/35

the same applies to fractions with variables…

8/3a = ?/18a²

What do you multiply 3a by to obtain 18a²?   6a

so you must multiply both by 6a    

 Complete:

   

You notice that you need to multiply the denominator by (x +1) so you must do the same to the numerator.

When you add or subtract fractions with different denominators, you will find that using the Least Common Denominator (LCD)  will simplify your work

Find the LCD of:

First factor each denominator completely. Factor Integers into primes!

6x - 30 = 6(x - 5)= 2·3(x - 5)

9x - 45 = 9(x - 5) = 3∙3(x - 5)

Form the product of the greatest power of each
(Remember that the LCM is the product of every factor to its greatest power)

2·3²(x - 5) = 18(x - 5)

Therefore the LCD is 18( x – 5)

Re write the following with their LCD

x² - 8x +16 = (x - 4)²

and

x²- 7x + 12 = (x - 4)(x - 3)

the LCD is (x -4)²(x -3)

Now rewrite each fraction using the LCD

 and